算法题目分类
根据《算法笔记》一书,对PAT甲级、乙级真题和codeup部分试题进行分类。
1. C/C++快速入门
1.1 数组
1.2 指针
1.3 结构体的使用
2. 入门模拟
2.1 简单模拟
不涉及算法,只是根据题目描述来编写代码,考察代码能力。
| 题目 | 解题关键 |
|---|---|
| codeup 问题 B: A+B | \ |
| B1001 害死人不偿命的(3n+1)猜想 | \ |
| B1010 一元多项式求导 | \ |
| B1011 A+B和C | \ |
| B1012 数字分类 | 有条不紊地整理 |
| B1016 部分A+B | \ |
| B1018 锤子剪刀布 | 注意scanf留在缓冲区的换行符\n的处理 |
| B1026 程序运行时间 | \ |
| B1032 挖掘机技术哪家强 | 统计各学校总分的方式 |
| B1046 划拳 | \ |
| A1002 A+B for Polynomials | 非零系数项个数的统计 |
| A1009 Product of Polynomials | 第二个多项式可边读边处理 |
| A1042 Shuffling Machine | 将扑克顺序号转为实际牌号的方式 |
| A1046 Shortest Distance | 便于计算距离的方式 |
| A1065 A+B and C (64bit) | B1011 A+B 和 C 进阶版 负数相加若溢出,可能得到0 |
2.2 查找元素
查找是学习写代码的一项基本功。
- 一般来说,如果需要在一个比较小范围的数据集内内进行查找,直接遍历即可。
- 如果需要查找的范围较大,可以用二分查找等算法进行更快速的查找
| 题目 | 解题关键 |
|---|---|
| B1004 成绩排名 | \ |
| B1028 人口普查 | 1. 不合理年龄的判断方式 2. 需要考虑全不合理的情况 |
| B1032 挖掘机技术哪家强 | 统计各学校总分的方式 |
| B1041 考试座位号 | \ |
| A1011 World Cup Betting | \ |
| A1006 Sign In and Sign Out | 方法类似 B1028 人口普查 |
| A1036 Boys vs Girls | \ |
2.3 图形输出
做法一般有两种:
- 通过规律,直接进行输出
- 定义一个二维字符数组,通过规律填充,然后输出整个二维数组
| 题目 | 解题关键 |
|---|---|
| B1027 打印沙漏 | 沙漏高度和符号数量的关系 |
| B1036 跟奥巴马一起编程 | \ |
| A1031 Hello World for U | 根据 n1和n3为 $\leq$ n2,且满足 n1+n2+n3 = N+2 的最大值,求出n1,n2,n3 |
2.4 日期处理
需要处理好平年和闰年、大月和小月的问题,需要细心处理。
闰年的判断方法:
非整百年:能被4整除为闰年
整百年:能被400整除的是闰年(1900年不是闰年)
2.5 进制转换
对一个P进制的数,如果要转换为Q进制,需要分两步:
将 P进制数x 转换为 十进制数y
int y = 0, pro = 1; while(x != 0) { y += (x % 10) * pro; x /= 10; pro *= p; }将 十进制数y 转换为 Q进制数z
采用除基取余法
int z[40], num = 0; //数组z 存放 Q进制数y 的每一位,num为位数 do { z[num++] = y % Q; //除基取余 y /= Q; } while(y != 0);使用
do···while语句而不是while的原因是:如果十进制数y = 0,使用while语句将使循环直接跳出,导致结果出错。
| 题目 | 解题关键 |
|---|---|
| B1022 D进制的A+B | 除基取余法 |
| B1037 在霍格沃茨找零钱 | \ |
| A1019 General Palindromic Number | \ |
| A1027 Colors in Mars | \ |
| A1058 A+B in Hogwarts | 题型同 乙级1037 在霍格沃茨找零钱 单位转换过程可能会超过int范围 |
2.6 字符串处理
考察代码能力的题型。一般需要仔细分析清楚题目中的输入和输出格式才能顺利AC。
有些题目中,可能实现逻辑非常麻烦,有很多细节和边界情况,此类题目需要多做多想,积累经验。
| 题目 | 解题关键 |
|---|---|
| B1002 写出这个数 | 数字转为字符串: C语言: sprintf(str, "%d", num)C++: to_string(num) |
| B1006 换个格式输出整数 | \ |
| B1009 说反话 | 句子颠倒,单词本身不颠倒 C++ 待更新 |
| B1014 福尔摩斯的约会 A1061 Dating |
正确归纳解码方式 |
| B1021 个位数统计 | \ |
| B1024 科学计数法 A1073 Scientific Notation |
1. 利用正则表达式,分开读取 数字部分 和 指数部分 2. 指数 < 0:整数部分必然为 0 3. 指数 >= 0: - 仍有小数点,何时输出小数点 - 没有小数点,后续输出0 |
| B1031 查验身份证 | \ |
| B1048 数字加密 | 1. 对齐两个整数 - 若加密正整数A 比 B 长,B高位补0后进行加密 - 若加密正整数A 比 B 短,B多余的部分正常输出,等同于A高位补0后进行加密 2. 结果从数字高位(字符串低位)开始输出 |
| A1001 A+B Format | 从数字高位(字符串低位)开始,需要添加,的位置满足**(i + 1) % 3 == len % 3 且 不是最后一位** |
| A1005 Spell It Right | \ |
| A1035 Password | (待优化) |
| A1077 Kuchiguse | 1. 通过reverse()反转字符串,将后缀转换为前缀,便于比较2. getline()之前注意读取换行符。 |
| A1082 Read Number in Chinese | 1. 四位数字分为一节,单位为个、万、亿 2. 一节中数字全为0,则不输出节的单位 3. 节中第一个非零数之前有0,则输出1个0 |
3. 算法初步
3.1 排序
3.1.1 简单选择排序($O(n^2)$)
简单选择排序是指,对一个序列A中的元素A[0] ~ A[n-1],令i从 0 到 n-1 枚举,进行 n 趟操作,每一趟从待排部分$[i, n-1]$中选择最小元素(记录下标),令其与待排部分的**第一个元素A[i]**进行交换,使得$[0, i]$区间有序。
void selectSort(int A[]) { //降序 简单选择排序
for(int i = 0; i < n; i++) {
int k = i;
for(int j = i; j < n; j++) { //选出最小的元素
if(A[j] < A[i])
k = j; //记录更小元素的下标
}
int tmp = A[i]; //交换A[k]与A[i]
A[i] = A[j];
A[j] = tmp;
}
}3.1.2 直接插入排序($O(n^2)$)
直接插入排序是指,对序列A的n个元素A[0]~A[n-1],令 i **从 1 **到 n-1 枚举,进行 n - 1 趟操作。
某一趟时,序列A的前 i 个元素 A[0]~A[i-1]已经有序,则该趟在范围$[0, i - 1]$中,从后往前寻找某个位置j,使得A[i]插入后,范围$[0, i]$有序(A[j]~A[i]后移一位)。
void insertSort(int A[]) { //升序 直接插入排序
for(int i = 1; i < n; i++) {
int tmp = A[i], j = i;
//从后往前遍历,便于编写代码
while(j > 0 && tmp < A[j - 1]) {
A[j] = A[j - 1];
j--;
}
A[j] = tmp;
}
}3.1.3 冒泡排序($O(n^2)$)
冒泡排序的本质在于交换,即每次通过交换的方式把当前剩余元素的最大值(升序)移动到一端,当剩余元素减少到0时,排序结束。整个过程执行 n-1 趟,每一趟从左到右依次比较相邻的元素,如果大的数在左边,则交换,该趟结束时,最大数被移动到当前剩余数的最右边。
void bubbleSort(int A[]) { //升序 冒泡排序
for(int i = 1; i < n; i++) {//进行 n - 1 趟排序
for(int j = 0; j < n - i; j++) {
if(a[j] > a[j + 1]) {
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
}
}
}
}3.1.4 排序题与sort函数的应用
PAT中的排序题,大部分只需要得到排序的最终结果,而不需要去写排序的完整过程(例如冒泡排序、快速排序等),因此推荐直接使用C语言的库函数qsort或是C++的sort函数进行排序。qsort函数的使用需要运用指针,且写法上没有sort函数简洁。sort函数根据具体情形使用不同的排序方法,效率较高,在实现中规避了经典快速排序中可能出现的会导致实际复杂度退化到$O(n^2)$的极端情况。
因此更推荐使用C++的sort函数进行代码编写。
结构体数组的排序
struct node { int x; int y; } ssd[10];如果想先按x从大到小排序,在x相等的情况下,按y从小到大排序(即二级排序),cmp的写法是:
bool cmp(node a, node b) { //返回值为true时,a排在b之前 if(a.x != b.x) { return a.x > b.x; //降序 } else { return a.y < b.y; //升序 } }排名的实现
很多排序题要求在排序之后计算每个个体的排名,规则一般是:分数相同的排名相同,占用一个排位。例如有5个学生的分数分别为90、88、88、88、86,其排名分别为1、2、2、2、5。
方法:
将第一个个体排名记为1,遍历剩余个体,如果当前分数等于上一个个体的分数,则当前个体排名等于上一个个体的排名,否则当前个体的排名等于数组下标+1
| 题目 | 解题关键 |
|---|---|
| B1015 德才论 A1062 Talent and Virtue |
设置flag作为考生的分类,便于所有考生统一排序 |
| A1012 The Best Rank | 1. 利用全局变量设计cmp函数 2. 通过记录所有科目的排名,最后选出最好的排名以及对应科目 3. 相同分数者排名相同,下一不同分数者排名为数组下标+1 |
| A1016 Phone Bills | (待优化) 1. 通话记录统一先排序后处理 2. 连续的两个通话记录,判断是否为 同一用户 且 为先通话后挂断的状态 3. 通话时长的统计方法 4. 单位美分cents 要转换为 美元$ |
| A1025 PAT Ranking | \ |
| A1028 List Sorting | \ |
| A1055 The World’s Richest | 超时问题。要求输出的人数$\leq$100,通过筛去每个年龄多余的人解决 |
| A1075 PAT Judge | (待优化) 1. 不能编译的提交得分为0 2. 没有提交过的答案需要输出为 -,利用<cstring>中的memset函数,为 得分数组 赋值 -1,表示没有提交过答案3. 没有任何一题通过编译 或 没有提交过答案的人不记录排名,设置 是否有通过编译的标识,进行筛选 4. 读取数据时,将用户数组下标看作id,便于统计 5. 排序以 是否有通过编译 为 第一排序条件 |
| A1080 | |
| A1083 | |
| A1095 |
3.2 散列
3.2.1 散列(hash)的定义与整数散列
例题:
给出$N$个正整数,再给出$M$个正整数,问这$M$个数中的每个数分别是否在$N$个数中出现过,其中 $N, M \leq10^5$,且所有正整数均不超过$10^5$。例如 $N = 5,M = 3$, $N$个正整数为 ${8, 3, 7, 6, 2}$,欲查询的$M$个正整数为 ${7, 4, 2}$。
对这个问题,最直观的思路是:对每个欲查询的正整数$x$,遍历所有$N$个数,看是否有一个数与$x$相等。这种做法的时间复杂度为$O(NM)$,显然不是好方法。可以采取用空间换时间的方式,用数组下标作为对应整数的标识,即设定一个bool型数组hashTable[100001],其中hashTable[x] == true表示正整数$x$在$N$个整数中出现过。这样就可以在一开始读入$N$个正整数时进行预处理。于是,对$M$个欲查询的数,就能直接通过hashTable数组判断出每个数是否出现过,这种做法的时间复杂度为$O(N+M)$。直接把输入的数作为数组的下标来对这个数的性质进行统计的方法非常实用,务必掌握。
但是这个方法有一个问题:如果输入的整数可能是$10^9$大小,甚至是字符串,就不能将其直接作为数组下标了。因此我们寻找一种做法,将元素通过一个函数转换为一个在能接受范围内的整数,使得该整数尽可能唯一地代表这个元素。这样的方法称为散列(hash),用于转换的函数称为散列函数H,也就是说,如果元素在转换前为key,那么转换后就是一个整数H(key)。
散列函数
对key是整数的情况来说,常用的散列函数有:
直接定址法
恒等变换,即
H(key) = key线性变换,即
H(key) = a * key + b
除留余数法
把
key除以一个数mod得到的余数作为hash值 的方法,即H(key) = key % mod通过这个散列函数,可以把很大的数转换为不超过 mod 的整数,这样就可以将它作为可用的数组下标。显然,当
mod是一个素数时,H(key)能尽可能覆盖[0,mod]范围内的每一个数。平方取中法(很少用)
取
key的平方的中间若干位作为hash值
冲突
当两个不同的数key1和key2他们的hash值相同时,这样的情况称为冲突。解决冲突的常用方法:
开放定址法(获取新的hash值)
线性探查法 (Linear Probing)
当表中下标为
H(key)的位置已经被其他元素占用,则检查下一个位置H(key)+1,以此类推。如果检查过程中超过了表长m,那么就回到表的首位继续循环,直到找到一个可用的位置,或是所有位置都已经被使用。H = (H(key) + i) % m;(i = 0, 1, 2, …, m-1)缺点:容易导致大量元素在相邻的散列地址上“聚集”(堆积),大大降低查找效率。
平方探查法 (Quadratic Probing)
当表中下标为
H(key)的位置已经被其他元素占用,则按如下顺序检查表中位置H = (H(key) + i) % m;i = $0, 1^2, -1^2, 2^2, -2^2, …, k^2, -k^2;(k \leq m/2)$可避免聚集问题。
缺点:不能探测到散列表上所有单元(但至少能探测到一半单元)。
再散列法(双散列法)
H = (H1(key) + i * H2(key)) % m;i 是冲突次数
链地址法 (拉链法)
不计算新的hash值,而是把 所有H(key)相同的key(称为同义词) 存储在一个线性链表中,由散列地址唯一标识。
一般来说,可以使用**标准库模板库中的map**来直接使用hash的功能(C++11以后可以用 unordered_map,速度更快),因此除非必须模拟这些方法或是对算法的效率要求比较高,一般不需要自己实现上面解决冲突的方法。
3.2.2 字符串hash初步
如果**key不是整数**,应该如何设计散列函数?
例题:
如何将一个二维整点$P$的坐标映射为一个整数,使得整点$P$可以由该整数唯一标识?
假设一个整点$P$的坐标是$(x,y)$,其中$0\leq x,y\leq Range$,那么可以令hash函数为H(P) = x * Range + y,这样对数据范围内的任意两个整点$P1$与$P2$,H(P1)都不会等于H(P2),就可以用H(P)来唯一地标识该整点P,接着便可以通过整数hash的方法进一步映射到较小的范围。
字符串hash是指将一个字符串S映射为一个整数,使得该整数可以尽可能唯一地代表字符串S。
为了讨论问题方便,假设字符串均由大写字母A~Z构成,不妨把 AZ 视为 025。接着按照26进制转换为10进制的思路,实现将字符串映射为整数的需求(转换成的整数最大为$26^{len}-1$,len为字符串长度)。
int hashFunc(char S[], int len) { //将字符串S转换为整数
int id = 0;
for(int i = 0; i < len; i++)
id = id * 26 + (S[i] - 'A'); //将26进制转换为10进制
return id;
}为了避免转换成的整数过大,需要注意 字符串长度len 不能太长。如果字符串中还有小写字母,可以把 AZ 作为 025,把 az 作为 2651,这样就变成了52进制转换为10进制的问题。
int hashFunc(char S[], int len) {
int id = 0;
for(int i = 0l i < len; i++) {
if(isupper(S[i])) {
id = id * 52 + (S[i] - 'A');
} else if(islower(S[i])) {
id = id * 52 + (S[i] - 'a');
}
}
return id;
}如果字符中还有数字,一般有两种处理方法:
按照小写字母的处理方法,增大进制数至62。
如果保证在字符串的末尾是个确定的数字,就可以把前面英文字母的部分按上面的思路转换成整数,再将末尾的数字直接拼接上去。
int hashFunc(char S[], int len) { int id = 0; for(int i = 0; i < len - 1; i++) id = id * 26 + (S[i] - 'A'); id = id * 10 + (S[len - 1] - '0'); return id; }
例题:
给出N个字符串(由三位大写字母组成),再给出M个查询字符串,问每个查询字符串在N个字符串中出现的次数。
#include <iostream>
using namespace std;
int hashFunc(char S[], int len) { //将字符串S转换为整数
int id = 0;
for(int i = 0; i < len; i++)
id = id * 26 + (S[i] - 'A'); //将26进制转换为10进制
return id;
}
int main() {
int N, M;
int hashTable[26 * 26 * 26] = {0};
cin >> N >> M;
string S[N];
for(int i = 0; i < N; i++) {
cin >> S[i];
int id = hashFunc(S[i], 3);
hashTable[id]++; //字符串出现的次数+1
}
string tmp;
for(int i = 0; i < M; i++) {
cin >> tmp;
int id = hashFunc(tmp, 3);
cout << hashTable[id] << endl; //输出字符串出现的次数
}
return 0;
}3.2.3 相关习题
| 题目 | 解题关键 |
|---|---|
| B1005 继续(3n+1)猜想 | 奇数在判断过程中,可能大小会超过100 |
| B1029 旧键盘 A1084 Broken Keyboard |
待优化 |
| B1033 旧键盘打字 | 不能用scanf或cin读取字符串,应采用gets(str)或getline(cin, str),因为题目只保证第 2 行输入的文字串非空 |
| B1038 统计同成绩学生 | \ |
| B1039 到底买不买 A1092 To Buy or Not to Buy |
\ |
| B1042 字符统计 | \ |
| B1043 输出PATest | \ |
| B1047 编程团体赛 | \ |
| A1041 | |
| A1050 | |
| A1048 |
3.3 递归
3.3.1 分治
分治(divide and conquer)的全称为“分而治之”。分治法将原问题划分成若干个规模较小而结构与原问题相同或类似的子问题,然后分别解决这些子问题,最后合并子问题的解,即可得到原问题的解。分治法的三个步骤:
- 分解:将原问题分解为若干和原问题拥有相同或相似结构的子问题。
- 解决:递归求解所有子问题。如果存在子问题的规模小到可以直接解决,就直接解决它。
- 合并:将子问题的解合并为原问题的解。
分治法分解出的子问题应当是相互独立、没有交叉的。如果存在两个子问题有相交部分,就不应该使用分治法解决。分治法作为一种算法思想,既可以使用递归的手段实现,也可以通过非递归的手段实现。一般来说,使用 递归 实现较为容易。
3.3.2 递归
递归很适合用来实现分治思想。
递归的逻辑中一般有两个重要概念:
- 递归边界
- 递归调用
其中递归调用是将原问题分解为若干个子问题的手段,而递归边界则是分解的尽头。递归的代码结构中一定存在这两个该概念,它们支撑起了整个递归最关键的逻辑。
经典例子1:使用递归求解n的阶乘
#include <iostream>
using namespace std;
int F(int n) {
if(n == 0) {
return 1;
} else {
return n * F(n-1);
}
}
int main() {
int n;
cin >> n;
cout << F(n) << endl;
return 0;
}经典例子2:求 Fibonacci 数列的第n项
Fibonacci 数列(即斐波那契数列) 是满足 F(0) = 1, F(1) = 1, F(n) = F(n-1) + F(n-2) (n $\geq$ 2) 的数列,数列的前几项为 1, 1, 2, 3, 5, 8, 13, 21, … 。
从定义中可以获知递归边界为 F(0) = 1 和 F(1) = 1,且递归调用为 F(n) = F(n-1) + F(n-2) (n $\geq$ 2) ,因此可以仿照求解n的阶乘的写法。
#include <iostream>
using namespace std;
int F(int n) {
if(n == 0 || n == 1) { //递归边界
return 1;
} else {
return F(n-1) + F(n-2);
}
}
int main() {
int n;
cin >> n;
cout << F(n) << endl;
return 0;
}最后来看全排列(Full Permutation)。全排列指n个整数能形成的 所有排列。
现在需要按字典序从小到大的顺序输出$1\sim n$的全排列,其中$(a_1, a_2, …, a_n)$的字典序小于$(b_1, b_2, …, b_n)$是指存在一个$i$,使得$a_1=b_1$、$a_2 = b_2$、…、$a_{i-1} = b_{i-1}$、$a_i < b_i$成立。
从递归的角度考虑,就可以分为若干个子问题:“输出以1开头的全排列”、“输出以2开头的全排列” … “输出以n开头的全排列”。不妨设定一个数组P,用来存放当前的排列;再设定一个散列数组hashTable,其中hashTable[x],当整数x已经在数组P中时,为1。
按顺序往P的第1位到第n位中填入数字。不妨假设当前已经填好了P[1] ~ P[index-1],正准备填P[index]。显然需要枚举 1 ~ n,如果当前枚举的数字x还没有在P[1] ~ P[index-1]中(即hashTable[x] == 0),那么就把它填入P[index],同时将hashTable[x]置为1,然后去处理P的第index + 1位(即进行递归);当递归完成时,再将hashTable[x]还原为0,以便让P[index]填下一个数字。
那么递归边界是什么呢?显然,当index达到n + 1时,说明P的的第1 ~ n位都已经填好了,此时可以把数组P输出,表示生成了一个排列,然后直接return即可。下面给出n = 3时的代码:
#include <iostream>
using namespace std;
void generateP(int index, int n) {
if(index == n + 1) { //递归边界,已经处理完排列的 1~n 位
for(int i = 1; i <= n; i++)
cout << P[i];
cout << endl;
return;
}
for(int x = 1; x <= n; x++) { //枚举 1~n,试图将 x 填入 P[index]
if(hashTable[x] == 0) { //如果 x 不在 P[1] ~ P[index - 1] 中
P[index] = x; //令 P 的第 index 位为 x,即把x加如当前排列
hashTable[x] = 1; //记 x 已在 P 中
generateP(index + 1, n); //处理排列的第 index + 1 号位
hashTable[x] = 0; //已处理完 P[index] 为 x 的子问题,还原状态
}
}
}
int main() {
int n = 3, P[11], hashTable[11] = {0};
generateP(1); //从P[1]开始填
return 0;
}最后的最后来看**$n$皇后问题**。$n$皇后问题是指在一个$nn$的国际象棋棋盘上放置$n$个皇后,使得这$n$个皇后*两两均不在同一行、同一列、同一条对角线上,求合法的方案数。
对于这个问题,如果采用组合数的方式来枚举每一种情况(即从$n^2$个位置中选择$n$个位置),那么需要$C_{n\times n}^n$的枚举量。但是换个思路,考虑到每行只能放置一个皇后、每列也只能放置一个皇后,如果把n列皇后所在的行号依次写出,那么就会是$1 \sim n$的一个排列。于是只需要枚举$1 \sim n$的所有排列,查看每个排列对应的放置方案是否合法,统计其中合法的方案即可。
于是可以在全排列的代码基础上进行求解。由于当达到递归边界时表示生成了一个排列,所以需要在起内部判断是否为合法方案,即遍历每两个皇后,判断它们是否在同一条对角线上(显然不在同一行和同一列),若不是,则累计计数变量cnt即可。主要代码如下:
int cnt = 0;
void generateP(int index) {
if(index == n + 1) { //递归边界,生成一个排列
int flag = 1; //flag为true表示当前排列为一个合法方案
for(int i = 1; i <= n; i++) { //遍历任意两个皇后
for(int j = i + 1; j <= n; j++) {
if(abs(i - j) == abs(P[i] - P[j])) //如果在一条对角线上
flag = 0;
}
}
if(flag) //当前方案合法
cnt++;
return;
}
for(int x = 1; x <= n; x++) {
if(hashTable[x] == 0) {
P[index] = x;
hashTable[x] = 1;
generateP(index + 1);
hashTable[x] = 0;
}
}
}这种枚举所有情况,然后判断每一种情况是否合法的朴素做法称为暴力法。
通过思考可以发现,当已经放置了一部分皇后时,可能剩余的皇后无论怎样放置都不可能合法,就不需要继续递归,直接返回上层即可。这种做法称为回溯法。
void generateP(int index) {
if(index == n + 1) { //递归边界,生成一个 合法方案
cnt++;
return;
}
for(int x = 1; x <= n; x++) { //第 x 行
if(hashTable[x] == 0) { //第 x 行还没有皇后
int flag = 1; //flag 为 1 表示当前皇后不会和之前的皇后冲突
for(int pre = 1; pre < index; pre++) { //遍历之前的皇后
if(abs(index - pre) == abs(x - P[pre])) {
flag = 0; //与之前的皇后在一条对角线冲突
break;
}
}
if(flag) { //如果可以把皇后放在第 x 行
P[index] = x; //令第 index 列皇后的行号为 x
hashTable[x] = 1; //第 x 行已被占用
generateP(index + 1); //递归处理第 index + 1 行皇后
hashTable[x] = 0; //递归完毕,还原第 x 行 为 为占用
}
}
}
}3.4 贪心
3.4.1 简单贪心
贪心法是求解一类最优化问题的方法,它总是考虑在当前状态下局部最优(或较优)的策略,来使全局的结果达到最优(或较优)。要获得最优结果,要求中间的每步策略都是最优的,因此严谨使用贪心法来求解最优化问题需要对采取的策略进行证明。证明的一般思路是使用反证法及数学归纳法,即假设策略不能导致最优解,然后通过一系列推导来得到矛盾,以此证明策略是最优的,最后用数学归纳法保证全局最优。不过对平常使用来说,也许没有时间或不太容易对想到的策略进行严谨的证明(贪心的证明往往比贪心本身更难),因此一般来说,如果在想到某个似乎可行的策略,并且自己无法举出反例,那么就勇敢的实现它。
3.4.2 区间贪心
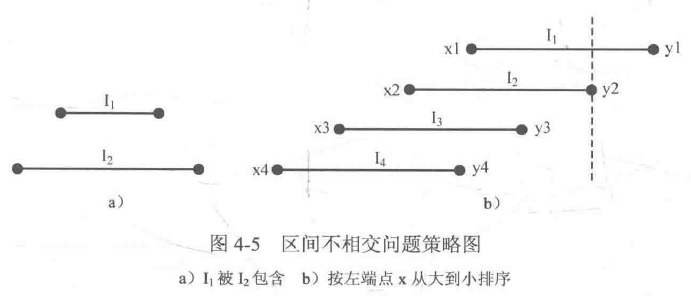
区间不相交问题:给出$N$个开区间$(x, y)$,从中选择尽可能多的开区间,使得这些开区间两两没有交集。例如对开区间$(1, 3)$、$(2,4)$、$(3, 5)$、$(6, 7)$来说,可以选出最多三个区间$(1, 3)$、$(3, 5)$、$(6, 7)$,它们互相没有交集。
首先考虑最简单的情况,如果开区间$I_1$被开区间$I_2$包含(如图4-5a所示),则选择$I_1$是最好的选择,因为这样就有更大的空间去容纳其他开区间。
接下来把所有开区间按左端点$x$从大到小排序,如果去掉区间包含的情况,那么一定有$y_1 > y_2 > … > y_n$成立(如图4-5b所示)。观察发现,$I_1$右边有一段一定不会和其他区间重叠,如果把它去掉,那么$I_1$的左边剩余部分就会被$I_2$包含,由图4-5a的情况可知,应当选择$I_1$。因此对这种情况,总是先选择 左端点最大 的区间。值得注意的是,总是先选择右端点最小的区间的策略也是可行的。
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 110;
struct Inteval {
int x, y; //开区间左右端点
} I[maxn];
bool cmp(Inteval a, Inteval b) {
if(a.x != b.x) { //先按左端点从大到小排序
return a.x > b.x;
else { //左端点相同的 按右端点从小到大排序
return a.y > b.y;
}
}
int main() {
int n;
while(cin >> n, n != 0) {
for(int i = 0; i < n; i++)
cin >> I[i].x >> I[i].y;
sort(I, I + n, cmp);
int cnt = 1, lastX = I[0].x; //记录不相交区间的个数,上一个被选中区间的左端点
for(int i = 1; i < n; i++) {
if(I[i].y <= lastX) { //如果该区间右端点在 lastX 左边
lastX = I[i].x; //以 I[i] 作为新选中的区间
cnt++; //不相交区间个数加1
}
cout << cnt << endl;
}
return 0
}与这个问题类似的是区间选点问题:给出$N$个闭区间$[x, y]$,求最少需要确定多少个点,才能使每个闭区间中都至少存在一个点。例如对闭区间$[1,4]$、$[2, 6]$、$[5, 7]$来说,需要两个点(例如3、5)才能保证每个闭区间内都有至少一个点。
事实上,这个问题和区间不相交问题的策略是一致的。首先,回到图4-5a,如果闭区间$I_1$被闭区间$I_2$包含,那么在$I_1$中取点可以保证这个点一定在$I_2$内。接着把所有区间按左端点从大到小排序,去除掉区间包含的情况,就可以得到图4-5b。由于每个闭区间中都需要存在一个点,因此对左端点最大的区间$I_1$来说,取左端点就能让它尽可能多地覆盖其他区间。区间选点问题的代码只需要把区间不想交问题代码中的I[i].y <= lastX改为I[i].y < lastX即可。
总的来说,不是所有问题都适合使用贪心法,但是这并不妨碍贪心算法称为一个简洁、实用、高效的算法。
3.4.3 相关习题
| 题目 | 解题关键 |
|---|---|
| B1020 月饼 A1070 Mooncake |
库存量和售价都应该定义为double类型 |
| B1023 组个最小数 | \ |
| A1033 To Fill or Not to Fill | 能到达的距离内,由近到远遍历,有三种情况: 1. 最近距离的加油站都到不了 2. 出现油价比目前低的加油站,就直接去 2.1 油不够,只加能刚好到达的油量 2.2 不用加油 3. 没有更低价的加油站,就加满油(能尽量少加更贵的油),去价格相对 最低的加油站 |
| A1037 | |
| A1038 | |
| A1067 |
3.5 二分
3.5.1 二分查找
二分查找的高效之处在于,每一步都可以去除当前区间中的一半元素,因此其时间复杂度是$O(\log n)$,这是十分优秀的。
在严格递增序列中查找给定的数$x$的做法:
#include <iostream>
using namespace std;
int binarySearch(int A[], int left, int right, int x) {
int mid;
while(left <= right) {
mid = (left + right) / 2;
if(A[mid] == x) {
return mid;
} else if(A[mid] > x) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1; //查找失败
}
int main() {
int A[n] = {1, 3, 4, 6, 7, 8, 10, 11, 12, 15};
printf("%d %d\n", binarySearch(A, 0, n - 1, 6), binarySearch(A, 0, n - 1, 9));
return 0;
}需要注意的是,如果过二分上界超过int型数据范围的一半,当欲查询元素在序列较靠后位置时,语句mid = (left + right) / 2中的left + right就有可能超过int而导致溢出,通常使用等价语句mid = left + (right - left) / 2作为代替,以避免溢出。另外,二分法可以使用递归进行实现,但在程序设计时,更多采用非递归的写法。
接下来探讨更进一步的问题:如果递增序列$A$中的元素可能重复,那么如何对给定的欲查询元素$x$,求出序列中第一个$\geq x$的元素位置$L$以及第一个$>x$的元素的位置$R$,这样元素$x$在序列中的存在区间就是$[L, R)$。
例如对下标从0开始、有5个元素的序列${1,3,3,3,6}$来说,如果要查询3,则应当得到$L = 1$、$R = 4$;如果查询 5,则应当得到$L = R = 4$。如果序列中没有$x$,$L$和$R$也可以理解为 假设序列中存在$x$,则$x$应当在的位置。
先来考虑第一个小问:求序列中的第一个$\geq x$的元素位置。
- 若
A[mid] >= x,说明第一个$\geq x$的元素的位置一定在**mid处或mid的左侧,应往左子区间[left, mid]继续查询,即令right = mid** - 若
A[mid] < x,说明第一个$\geq x$的元素的位置一定在**mid右侧,应往右子区间[mid+1, right]继续查询,即令left = mid + 1**
int lower_bound(int A[], int left, int right, int x) {
int mid;
while(left < right) {
mid = (left + right) / 2;
if(A[mid] >= x) { //中间值 >= x
right = mid;
} else { //中间值 < x
left = mid + 1;
}
}
return left; //返回夹出来的位置
}上述代码有两个需要注意的地方:
- 循环条件为
left < right,而不是之前的left <= right,这是由问题本身决定的。因为如果想要返回第一个>= x的元素的位置,就不需要判断元素x本身是否存在。 - 二分的初始区间应当能覆盖到所有可能返回的结果,考虑到欲查询元素可能比序列中所有元素都大,此时应当返回n,因此二分上界是n,故二分的初始区间为
[left, right] = [0, n]。
接下来解决第二小问:求序列中第一个大于x的元素的位置。
int upper_bound(int A[], int left, itn right, int x) {
int mid;
while(left < right) {
mid = (left + right) / 2;
if(A[mid] > x) {
right = mid;
} else {
left = mid + 1;
}
}
return left; //返回夹出来的位置
}lower_bound和upper_bound函数都在解决这样一个问题:寻找有序序列中第一个满足某条件的元素的位置。这是一个非常重要且经典的问题,平时能碰到的大部分二分法问题都可以归结于这个问题。
3.5.2 二分法拓展
首先介绍如何计算$\sqrt2$的近似值。
对$f(x) = x^2$来说,在$x \in [1, 2]$范围内,$f(x)$随着$x$的增大而增大,这就给使用二分法创造了条件。
以精确到$10^{-5}$为例,令浮点型left和right的初值分别是 1 和 2,然后根据中点mid处$f(x)$的值与 2 的大小来选择子区间进行逼近:
- 若
f(mid) > 2,说明mid> $\sqrt2$,令right = mid - 若
f(mid) < 2,说明mid< $\sqrt2$,令left = mid
上面两个步骤当right - left < $10^{-5}$时结束,显然当left与right的距离 < $10^{-5}$ 时已满足精度要求,mid即为所求的近似值。
const double eps = 1e-5; //精度为 10^{-5},科学计数法
double f(double x) {
return x * x;
}
double calSqrt() {
double left = 1, right = 2, mid;
while(right - left > eps) {
mid = (left + right) / 2;
if(f(mid) > 2) { //即 mid > sqrt(2)
right = mid;
} else {
left = mid;
}
}
return mid;
}事实上,计算$\sqrt2$的近似值的问题是这样一个问题的特例:给定一个定义在$[L, R]$上的单调函数$f(x)$,求方程f(x) = 0的根。
同样假设精度要求为eps = $10^{-5}$,函数$f(x)$在$[L,R]$上递增,令left与right的初值分别为$L$、$R$。根据中点mid的函数值f(mid) 与 0 的大小关系来判断往哪个子区间继续逼近f(x) = 0的根:
- 若
f(mid) > 0,说明f(x) = 0的根在mid左侧,应往左子区间继续逼近,即令right = mid - 若
f(mid) < 0,说明f(x) = 0的根在mid右侧,应往右子区间继续逼近,即令left = mid
const double eps = 1e-5; //精度为 10^{-5},科学计数法
double f(double x) {
return ...;
}
double solve() {
double left = L, right = R, mid;
while(right - left > eps) {
mid = (left + right) / 2;
if(f(mid) > 0) {
right = mid;
} else {
left = mid;
}
}
return mid; //f(x) = 0 的根
}3.5.3 快速幂
3.5.4 相关习题
| 题目 | 解题关键 |
|---|---|
| A1010 Radix | 1. 基数上界为 已确认数字的十进制大小 + 1 与 下界中的较大值(确保不会出现多个解(而且基数不确定的数,只有一位数的时候才可能多个解) ) 2. 基数过大时,数值转换为十进制会发生上溢,存储结果为负数 |
| A1044 | |
| A1048 |
3.6 tow pointers
3.6.1 什么是two pointers
3.6.2 归并排序
3.6.3 快速排序
3.6.4 相关习题
| 题目 | 解题关键 |
|---|---|
| B1030 完美数列 A1085 Perfect Sequence |
\ |
| B1035 插入与归并 A1089 Insert or Merge |
1. 插入排序:未排序部分和初始序列一定相同 2. 归并排序:末尾不足数量的子序列同样需要排序 3. 插入排序 更容易判断,将其作为判断排序类型的切入点 4. 插入和归并排序的**实际操作由排序函数 sort/qsort**代替 |
| A1029 | |
| A1048 |
3.7 其他高效技巧与算法
3.7.1 打表
3.7.2 活用递推
3.7.3 随机选择法
3.7.4 相关习题
| 题目 | 解题关键 |
|---|---|
| B1040 有几个PAT A1093 Count PAT’s |
1. A前有P,后有T才能形成PAT; 2. 当前A能构成的PAT数量 = 之前P的数量 * 之后T的数量 3. 突破口:先遍历一遍,获取T的数量 |
| B1045 快速排序 A1101 Quick Sort |
1. 可能的主元:左侧的最大值比自身小;右侧的最小值比自身大 2. 输出即使没有主元,也得换行 |
4. 数学问题
4.1 简单数学
| 题目 | 解题关键 |
|---|---|
| B1003 | |
| B1019 A1069 |
|
| B1049 A1104 |
|
| A1008 | |
| A1049 |
4.2 最大公约数与最小公倍数
| 题目 | 解题关键 |
|---|---|
| B1008 |
4.3 分数的四则运算
| 题目 | 解题关键 |
|---|---|
| B1034 A1088 |
|
| A1081 |
4.4 素数
| 题目 | 解题关键 |
|---|---|
| B1007 | |
| B1013 | |
| A1015 | |
| A1078 |
4.5 质因子分解
| 题目 | 解题关键 |
|---|---|
| A1059 | |
| A1096 |
4.6 大整数运算
| 题目 | 解题关键 |
|---|---|
| A1023 | |
| A1024 |
4.7 扩展欧几里得算法
4.8 组合数
5. C++标准模板库介绍
5.1 vector
| 题目 | 解题关键 |
|---|---|
| A1039 | |
| A1047 |
5.2 set
| 题目 | 解题关键 |
|---|---|
| A1063 |
5.3 string
| 题目 | 解题关键 |
|---|---|
| A1060 |
5.4 map
| 题目 | 解题关键 |
|---|---|
| B1044 A1100 |
|
| A1022 | |
| A1054 | |
| A1071 |
5.5 queue
5.6 priority_queue
5.7 stack
5.8 pair
5.9 algorithm
6. 数据结构专题1
6.1 栈的应用
| 题目 | 解题关键 |
|---|---|
| A1051 Pop Sequence | 1. 可能会发生堆栈溢出 2. 栈顶元素和当前需要出栈的元素相同时,出栈。该判断之前必须先判断栈是否不为空(否则会报错) 3. 标记出栈序列中待出栈元素下标,最终标记只有超出序列下标,才可能是出栈序列 |
6.2 队列的应用
| 题目 | 解题关键 |
|---|---|
| A1056 Mice and Rice | 1. 输入的第二行是按老鼠的序号给出的重量。第三行给出的是老鼠的序号,而不是按序号给出的比赛序号 2. 用队列记录老鼠的序号(而不是记录老鼠的结构体,有利于减少内存的占用),晋级的老鼠重新入队 3. 最后的分组中,老鼠数量可能不足(利用<cmath>中的 ceil函数向上取整) |
6.3 链表处理
| 题目 | 解题关键 |
|---|---|
| B1025 反转链表 A1074 Reversing Linked List |
1. 通过数组下标来表示地址,便于链接各个节点 2. 可能存在无效结点 3. 只根据 链表顺序的地址 进行反转,有利于节约开销 |
| A1032 Sharing | \ |
| A1052 Linked List Sorting | 存在无有效结点的情况 |
| A1097 |
7. 搜索专题
7.1 深度优先搜索DFS
| 题目 | 解题关键 |
|---|---|
| A1103 Integer Factorization | 1. 利用vector(可根据size函数确认符合要求的元素个数),预先存储所有 ≤ N的 元素(整数的P次幂值)2. 为了保证底数最大的序列被选中,从大到小遍历 3. DFS函数的参数:当前元素下标,已选元素数量,已选元素之和,已选元素的底数之和 4. DFS函数的递归边界:已选元素数量为K且和为N 5. DFS函数的递归调用:选择当前元素和不选择当前元素 6. 剪枝:和超过N 或 已选元素数量超过K 或 遍历完底数序列时,不必再递归 |
7.2 广度优先搜索BFS
| 题目 | 解题关键 |
|---|---|
| A1091 Acute Stroke | 1. 设定相对当前位置的前后左右上下6个方向的增量,便于枚举 2. 设置数组 inq记录当前位置是否入过队3. 越界、当前位置为0、已入过队的位置无需再判断。 4. 在BFS函数中,利用队列进行BFS,使用STL的 queue,push函数只将所选元素的副本入队,后续对原元素的操作不改变队列中的副本。 |
8. 数据结构专题2
8.1 树与交叉树
8.2 二叉树的遍历
| 题目 | 解题关键 |
|---|---|
| A1020 Tree Traversals | \ |
| A1086 Tree Traversals Again | 先序序列相当于入栈次序;中序序列相当于出栈次序 |
| A1102 Invert a Binary Tree | 1. 题目给的是结点编号的关系,故采用静态链表存储二叉树 2. 反转二叉树即每个结点的左右子树对换,选择后序遍历 |
8.3 树的遍历
| 题目 | 解题关键 |
|---|---|
| A1004 Counting Leaves | 1. 利用数组存储每层的叶结点个数 2. 根据出队结点的层数,获取最大层数,遍历输出每层叶结点个数 |
| A1053 Path of Equal Weight | 1. 输出的路径序列要求降序,因此在读入结点时就将孩子节点按权重降序排序,这样,之后遍历时得到的路径即为降序 2. 利用 vector的begin和end函数获得vector的首元素地址和尾后地址,用于sort函数排序3. 利用 vector存储路径,在递归子结点之前,用push_back函数将子结点加入路径,递归回溯后,用pop_back将先前加入的子结点移出路径 |
| A1079 Total Sales of Supply Chain | 1. 静态写法表示树,即用数组下标指代结点 2. 结点的结构体中设有货物量变量,用来判断是否为零售商(本题采用了BFS;也可DFS) |
| A1090 Highest Price in Supply Chain | 由于不涉及结点的数据域,可以直接用vector<int> child[maxn]存放树 |
| A1094 | |
| A1106 |
8.4 二叉查找树BST
| 题目 | 解题关键 |
|---|---|
| A1043 Is It a Binary Search Tree | 1. 静态写法(变长数组)表示二叉树 2. 根据BST左子树所有结点的数据域 < 根结点的数据域,右子树所有结点的数据域 ≥ 根结点的数据域(由输入样例得出大小关系,镜像则相反),获取左右子树的边界,判断是否符合先序序列,若符合,则按照左右根的顺序递归,将符合的根结点存入 vector(获取后序序列)3. 若vecotr中元素数量 = 输入序列的元素数量(能顺利转换为BST的后序序列),说明输入序列为先序序列 |
| A1064 Complete Binary Search Tree | 1. 输入的元素升序排序,即为二叉树的中序遍历序列。 2. 静态写法(变长数组)按照层序存储完全二叉排序树 3. 对二叉树进行中序遍历,依次填入中序遍历序列的元素即可得到层序存储的二叉树。注意:中序遍历时,二叉树数组根结点的下标: 若设为1,则左右孩子结点下标为 root * 2和root * 2 + 1;若设为0,则左右孩子结点下标为 root * 2 + 1和root * 2 + 24. 顺序输出二叉树数组元素即为层序遍历序列 |
| A1099 Build A Binary Search Tree | 静态写法表示树,解题方法和 A1064 基本一致 |
8.5 平衡二叉树
| 题目 | 解题关键 |
|---|---|
| A1066 Root of AVL Tree | 即写出平衡二叉树的代码模板 1. 新建结点的初始高度为1 2. 获取树高时,注意递归到空结点时,返回0 3. 插入结点,递归过程中从系统栈出栈后: 1) 平衡因子为2时,树型可能为LR型或LL型,LR型需要先对当前结点的左子树进行右旋;之后,LR型和LL型都需要对当前结点进行右旋 2) 平衡因子为-2时,树型可能为RL型或RR型,RL型需要先对当前结点的右子树进行左旋;之后,RL型和RR型都需要对当前结点进行左旋 4. 左旋和右旋过程中要及时更新树高 |
8.6 并查集
| 题目 | 解题关键 |
|---|---|
| A1107 Social Clusters | 1. 根据共同(包括潜在的→有共同爱好的人另外的爱好)爱好来确定潜在朋友的集合,利用hobby[1001]记录 任意一个 拥有对应爱好的结点,便于合并操作2. 遍历各用户,根据根结点统计各集合的人数 3. 将集合按包含人数降序排序,再遍历即可筛选统计出集合个数 4. 路径压缩可选 |
8.7 堆
| 题目 | 解题关键 |
|---|---|
| A1098 Insertion or Heap Sort | 1. 用于表示树的数组,注意下标从 0或1 开始,孩子结点表示的区别 2. 插入排序:未排序部分和初始序列一定相同 3. 堆排序:后面的元素有序,前面无规律 4. 插入排序 更容易判断,将其作为判断排序类型的切入点 4. 插入排序的实际操作可由排序函数 sort实现5. 要用堆排序得到递增序列,则需要建立大根堆 6. 堆排序从后往前找到第一个 $<$ 堆顶的元素,与堆顶元素交换,再对整个堆向下调整 |
8.8 哈夫曼树
9. 图算法专题
9.1 图的定义和相关术语
9.2 图的存储
9.3 图的遍历
| 题目 | 解题关键 |
|---|---|
| A1013 Battle Over Cities | 1. 问题等价于求 一个无向图去掉一个结点后,连通分量的数量,这种问题一般有两种方法:图的遍历和并查集 2. cin会超时,需要改为scanf,邻接矩阵和邻接表都可存储图3. 每次输入被占领的城市之前,要重置城市的访问状态为未访问 4. 将失去的城市标记为已访问,即可达到失去的效果(没有公路可以到达) |
| A1021 | |
| A1034 Head of a Gang | 1. 相同人员之间可能多次通话 2. map<type1, type2>自动按type1从小到大输出,使用map<string, int>建立头目姓名与成员数量的关系,便于输出结果3. 图中可能有环,为了边权不被漏加,需要先累加边权再递归;同时为了防止边权被重复计算,累加后删除这条边,以免走回头路、重复计算边权 |
| A1076 Forwards on Weibo | 1. 转发是粉丝转发博主的信息,因此要根据用户的关注情况建立从博主到粉丝(即反向)的有向图 2. DFS记录访问过的结点数量比较麻烦,BFS比较方便 3. 可能形成环 ,必须控制每个用户只能转发一次(遍历时只能访问一次) |
9.4 最短路径
| 题目 | 解题关键 |
|---|---|
| A1003 Emergency | |
| A1018 | |
| A1030 Travel Plan | |
| A1072 | |
| A1087 |