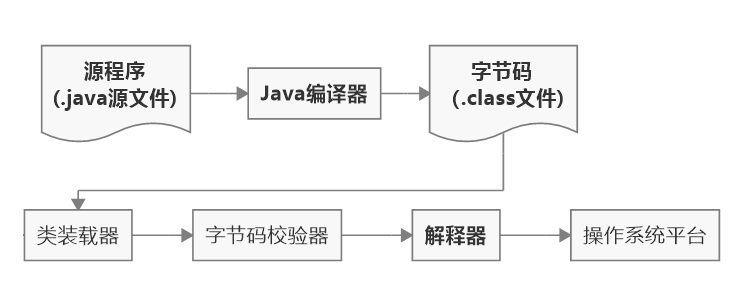
Python和Java一样大小写敏感。
变量和简单数据类型
字符串
在Python中,用引号(可以是单引号,也可以是双引号)括起的都是字符串。
使用方法修改字符串的大小写
合并(拼接)字符串
Python使用+来合并字符串。
使用方法删除多余的空格
strip():
删除字符串首尾空格
lstrip():
删除字符串开头的空格
rstrip():
删除字符串末尾的空格
将字符串中的特定单词都替换为另一个单词
replace()
例子:
message = "I really like dogs."
message.replace('dog', 'cat')
Python2中的print语句
例如:print "Hello Python 2.7 world!"
无需将要打印的内容放在括号内。从技术上说,Python 3中的print是一个函数,因此括号必不可少。
数字
整数
Python用**表示次方运算
如3**2的结果为9。
浮点数
使用函数str()避免类型错误
str():将非字符串值表示为字符串
Python允许在数字中间以_分隔,提高可读性。
JDK7的特性:赋值时,可以用下划线_分割过长的数字(整数&浮点数均可),提高可读性。
注释
在Python中,用**井号#**标识注释。
列表简介
列表是什么
列表由一系列按特定顺序排列的元素组成,像一个栈。可以创建包含字母表中所有字母、数字、所有家庭成员姓名的列表,也可以加入任何东西,其中的元素之间可以没有任何关系。
在Python中,用方括号[]表示列表,并用逗号来分隔其中的元素。如:
bicycles = ['trek', 'cannondale', 'redline', 'specialized']
print(bicycles)
Python会打印列表的内部表示,包括方括号:
['trek', 'cannondale', 'redline', 'specialized']
访问列表元素
如bicycles[0],请求获取列表元素时,Python只返回该元素,而不包括方括号和引号,是整洁干净的输出。
还可以对任何列表元素调用字符串方法。
索引从0开始
使用列表中的各个值
可以像使用其他变量一样使用列表中的各个值。
修改、添加和删除元素
修改列表元素
指定列表名和要修改的元素的索引,再指定该元素的新值即可。如:
motorcycles = ['honda', 'yamaha', 'suzuki']
motorcycles[0] = 'ducati'
在列表中添加元素
在列表末尾添加元素:使用append()方法
motorcycles.append('ducati')
append()方法让动态地创建列表易如反掌。
在列表中插入元素:使用insert()方法(需要指定新元素的索引和值)
motorcycles.insert(0, 'ducati')
从列表中删除元素
使用del语句删除元素
知道要删除的元素在列表中的位置,可以用del语句。
del motorcycles[0]
删除元素后,其余元素索引会相应发生变动。
使用**方法pop()**删除元素
方法pop()可以删除列表末尾元素,并能让你接着使用它。
popped_motorcycle = motorcycle.pop()
弹出列表中任何位置处的元素
在方法pop()的括号中指定要删除元素的索引即可。
first_owned = motorcycles.pop(0)
使用方法remove()根据值删除元素
不知道要从列表中删除的值所处的位置,只知道要删除元素的值是,可以使用方法remove()。
方法remove()只删除第一个指定的值。如果要删除的值可能在列表中出现多次,就需要使用循环来判断是否删除了所有这样的值。
组织列表
使用方法sort()对列表进行永久性排序
- 无参数:按字母顺序排序
- 填入参数
reverse=True:按字母逆序排序
cars = ['bmw', 'audi', 'toyota', 'subaru']
cars.sort()
cars.sort(reverse=True)
print(cars)
并非所有的值都是小写时,按字母顺序排列列表要复杂些。决定排列顺序时,有多种解读大写字母的方式,要指定准确的排列顺序可能比较复杂。但是大多数排序方式都基于本节介绍的知识。
使用函数sorted()对列表进行临时排序
print(sorted(cars))
反转列表元素
cars.reverse()
确定列表的长度
len(cars)
使用列表时避免索引错误
错误示例:
motorcycles = ['honda', 'yamaha', 'suzuki']
print(motorcycles[3])
即类似其他语言的数组越界访问,会引起索引错误。
操作列表
遍历整个列表
语句为for xxx in xxx:(注意不要遗漏冒号)
例子:
magicians = ['alice', 'david', 'carolina']
for magician in magicians:
print(magician)
- 编写for循环时,对于用于存储列表中每个值的临时变量,可指定任何名称。
- Python根据缩进来判断代码行与前一个代码行的关系。在for循环后面,没有缩进的代码就不是循环的一部分。
避免缩进错误
- 两行独立的代码语句,如果不小心缩进,Python将会报错。
创建数字列表
使用函数range()
for value in range(1, 5):
print(value)
打印结果为:
1
2
3
4
即输出范围左闭右开。
习题:使用一个for循环打印数字1~20(含)
for value in range(1, 21):
print(value)
使用range()创建数字列表
- 要创建数字列表,可使用函数
list()将range()的结果直接转换成列表。
numbers = list(range(1,6))
even_numbers = list(range(2, 11, 2))
squares = []
for value in range(1,11):
squares.append(value**2)
对数字列表执行简单的统计计算
digits = [1, 2, 3, 4, 5, 6, 7, 8, 9, 0]
min(digits)
max(digits)
sum(digits)
列表解析
列表解析将for循环和创建新元素的代码合并成一行,并自动附加新元素。
如创建平方数列表可以写成:
squares = [value**2 for value in range(1, 11)]
要使用这种语法,首先指定一个描述性的列表名,如squares;然后定义一个表达式,用于生成要存储到列表中的值。
在上述例子中,表达式为value**2
使用列表的一部分
Python称列表的部分元素为切片。
切片
创建切片可指定要使用的第一个元素的索引和最后一个元素的索引+1(创建范围左闭右开)。
如:
players = ['charles', 'martina', 'michael', 'florence', 'eli']
print(players[0:3])
如果没有指定第一个索引,Python将自动从列表开头开始:
player[:4]
要让切片终止于列表末尾,也可通过省略终止索引实现。
player[2:]
如果想输出最后三名队员,可通过切片player[-3:]实现
遍历切片
for player in players[:3]:
print(player);
复制列表
要复制列表,可以通过同时省略起始索引和终止索引,创建一个包含整个列表的切片。
例如,假设有一个列表,其中包含你最喜欢的三种食品,而你还想创建另外一个列表,其中包含一位朋友喜欢的所有食物。不过你喜欢的视频,这位朋友都喜欢,因此可以通过复制来创建这个列表:
my_foods = ['pizza', 'falafel', 'carrot cake']
friend_foods = my_foods[:]
friend_foods = my_foods
元组
列表是可以修改的,非常适合用于存储在程序运行期间可能变化的数据集。但有时候需要创建一系列不可修改的元素,元组可以满足这种需求。
Python将不可变的列表称为元组。
定义元组
元组看起来犹如列表,但使用圆括号来标识。
例如有一个大小不应改变的矩形,可将其长宽存储在一个元组中:
dimensions = (200, 50)
遍历元组中的所有值
同遍历列表相同
修改元组变量
虽然不能修改元组中的元素,但可以给存储元组的变量赋值。因此如果要修改前述矩形的尺寸,可重新定义整个元组:
dimensions = (200, 50)
dimensions = (400, 100)
设置代码格式
PEP(Python Enhancement Proposal):Python改进提案。
PEP 8是最古老的PEP之一,提供了代码格式设置指南。
缩进
PEP 8建议每级缩进都使用四个空格,既提高可读性,又留下了足够的多级缩进空间。
在字处理文档中,大家常常使用 制表符 而不是 空格 来缩进。对于字处理文档来说,这样做的效果很好,但混合使用制表符和空格会让Python解释器感到迷惑。每款文本编辑器都提供了将输入的制表符转换为指定数量的空格的设置。在编写代码时应该使用制表符键,但一定要对编辑器进行设置,使其在文档中插入空格而不是制表符。
行长
建议每行不超过80字符,PEP 8还建议注释的行长都不超过72字符,因为有些工具为大型项目自动生成文档时,会在每行注释开头添加格式化字符。在大多数编辑器中,都可以设置一个视觉标志——通常是一条垂直参考线,让我们知道不能越过的界限在什么地方。
if 语句
条件测试
值为True或False的表达式被称为条件测试。
检查是否相等时,大小写的影响
在Python中检查是否相等时区分大小写,两个大小写不同的值会被视为不相等。
如果大小写无关紧要,可将变量的值转换为小写,再进行比较:
car = 'Audi'
car.lower() == 'audi'
检查多个条件
- 使用and检查多个条件(Java/C/C++ 中为 &&)
- 使用or检查多个条件(Java/C/C++ 中为 ||)
检查特定值是否包含在列表中
有时候,执行操作前必须检查列表是否包含特定的值。例如,结束用户的注册过程前,可能需要检查用户名是否已包含在用户名列表中。在地图程序中,可能需要检查用户提交的位置是否包含在已知位置列表中。
要判断特定的值是否已包含在列表中,可使用关键字in。
requested_toppings = ['mushrooms', 'onions', 'pineapple']
print('mushrooms' in requested_toppings)
检查特定值是否不包含在列表中
使用关键字not in。例如,如果有一个列表,其中包含被禁止在论坛上发表评论的用户,就可在允许用户提交评论前检查他是否被禁言:
banned_users = ['andrew', 'carolina', 'david']
user = 'marie'
if user not in banned_users:
print(user.title() + ", you can post a response if you wish.")
布尔表达式
布尔表达式不过是条件测试的别名。
布尔值通常用于记录条件,如游戏是否正在运行,或用户是否可以编辑网站的特定内容:
game_active = True
can_edit = False
if语句
简单的 if 语句
if conditional_test:
do something
假设有一个表示某人年龄的变量,而你想知道这个人是否够投票的年龄,可使用如下代码:
age = 19
if age >= 18:
print("You are old enough to vote!")
if - else 语句
age = 19
if age >= 18:
print("You are old enough to vote!")
else:
print("Sorry, you are too young to vote.")
if - elif - else 结构
在现实世界中,很多情况下需要考虑的情形都超过两个。
age = 12
if age < 4:
price = 0
elif age < 18:
price = 5
else:
price = 10
print("Your admission cost is $" + str(price) + ".")
使用if语句处理列表
检查特殊元素
requested_toppings = ['mushrooms'. 'green peppers', 'extra cheese']
for requested_topping in requested_toppings:
if requested_topping == 'green peppers':
print("Sorry, we are out of green peppers right now.")
else:
print("Adding " + requested_topping + '.')
print("\nFinished making your pizza!")
确定列表不是空的
requested_toppings = []
if requested_toppings:
for requested_topping in requested_toppings:
print("Adding " + requested_topping + '.')
print("\nFinished making your pizza!")
else:
print("Are you sure you want a plain pizza?")
- 在if语句中将 列表名 用在条件表达式中时,Python将在列表至少包含一个元素时返回True,并在列表为空时返回False。
使用多个列表
下列示例定义两个列表,其中第一个列表包含披萨店供应的配料,第二个列表包含顾客点的配料。这次对于顾客要求的每个配料,都检查是否时披萨店供应的配料:
avaliable_toppings = ['mushrooms', 'olives', 'green peppers',
'pepperoni', 'pineapple', 'extra cheese']
requested_toppings = ['mushrooms'. 'green peppers', 'extra cheese']
for requested_topping in requested_toppings:
if requested_topping in avaliable_toppings:
print("Adding " + requested_topping + ".")
else:
print("Sorry, we don't have " + requested_topping + ".")
print("\nFinished making your pizza!")
字典
列表:用方括号[]标识
元组:用圆括号()标识(不可修改)
字典:用花括号{}标识
使用字典
在Python中,字典是一系列 键-值 对。每个键都与一个值相关联,可以使用键来访问与之相关联的值,可以将任何Python对象用作字典中的值。
键和值之间用冒号:分隔,键-值对之间用逗号分隔。如:alien_0 = {'color': 'green', 'points': 5}
访问字典中的值
要获取与键相关联的值,可依次指定字典名和放在方括号内的键。
如:
alien_0 = {'color': 'green', 'points': 5}
new_points = alien_0['points']
添加 键-值 对
字典是一种动态结构,可随时添加 键-值 对。要添加 键-值 对,可依次指定字典名、用方括号括起的键和相关联的值。
如:
alien_0['x_position'] = 0
alien_0['y_position'] = 25
- 键-值 对的排列顺序与添加顺序不同。Python只关心 键-值 对之间的关联关系。
先创建一个空字典
可先使用一对空的花括号定义一个字典,再分行添加各个 键-值 对。
使用字典来存储用户提供的数据或在编写能自动生成大量 键-值 对的代码时,通常都需要先定义一个空字典。
修改字典中的值
修改字典中的值,可依次指定字典名、用方括号括起的键以及与该键相关联的新值。
删除 键-值 对
对于字典中不再需要的信息,可使用del语句将相应的 键-值 对彻底删除。使用del语句时,必须指定字典名和要删除的键。
如:
del alien_0['points']
由类似对象组成的字典
字典可以存储一个对象的多种信息,也可以存储众多对象的同一种信息。
favorite_languages = {
'jen': 'python',
'sarah': 'c',
'edward': 'ruby',
'phil': 'python',
}
遍历字典
遍历所有的 键-值 对
user_0 = {
'username': 'efermi'.
'first': 'enrico',
'last': 'fermi',
}
for key, value in user_0.items():
print("\nKey: " + key)
print("Value: " + value)
如例子所示,要编写用于遍历字典的for循环。可声明两个变量用于存储键和值,这两个变量可以使用任何名称。
- 方法
items()返回一个 键-值 对列表
- 即使遍历字典时,键-值 对的返回顺序也与存储顺序不同。
遍历字典中的所有键
下面遍历一下字典中的名字,但在名字为指定朋友的名字时,打印一条消息,指出其喜欢的语言:
friends = ['phil', 'sarah']
for name in favorite_languages.keys():
print(name.title())
if name in friends:
print(" Hi " + name.title() +
", I see your favorite language is " +
favorite_languages[name].title() + "!")
还可以使用keys()确定某个人是否接受了调查:
if 'erin' not in favorite_languages.keys():
print("Erin, please take our poll!")
方法keys()并非只能用于遍历,实际上,它返回一个包含字典中所有键的列表。
按顺序遍历字典中的所有键
要以特定的顺序返回元素,一种办法是在for循环中对返回的键进行排序。为此,可以使用函数sorted()(临时排序)来获得按特定顺序排列的键列表的副本。
for name in sorted(favorite_languages.keys()):
print(name.title() + ", thank you for taking the poll.")
遍历字典中的所有值
嵌套
在列表中存储字典
字典alien_0包含一个外星人的各种信息,但无法存储第二个外星人的信息。如何管理成群结队的外星人呢?一种办法是创建一个外星人列表,其中每个外星人都是一个字典,包含有关该外星人的各种信息(即字典列表)。
aliens = []
for alien_number in range(0, 30):
new_alien = {'color': 'green', 'points': 5, 'speed': 'slow'}
aliens.append(new_alien)
for alien in aliens[:5]:
print(alien)
print("...")
print("Total number of aliens: " + str(len(aliens)))
在字典中存储列表
有时候,需要将列表存储在字典中。例如,你要如何描述顾客点的披萨呢?如果使用列表,只能存储要添加的披萨配料;但使用字典,还可以包含其他有关披萨的描述。
pizza = {
'crust': 'thick',
'toppings': ['mushrooms', 'extra cheese'],
}
for topping in pizza['topping']:
print("\t" + topping)
- 每当需要在字典中将一个键关联到多个值时,都可以在字典中嵌套一个列表。
在本章前面有关喜欢的编程语言的示例中,如果将每个人的回答都存储在一个列表中,被调查者就可以选择多种喜欢的语言。因此,在遍历该字典的for循环中,我们需要再使用一个for循环来遍历与被调查者相关联的语言列表:
favorite_languages = {
'jen': ['python', 'ruby'],
'sarah': ['c'],
'edward': ['ruby', 'go'],
'phil': ['python', 'haskell'],
}
for name, languages in favorite_languages.items():
print("\n" + name.title() + " 's favorite languages are:")
for language in languages:
print("\t" + language.title())
在字典中存储字典
可以在字典中嵌套字典,但这样做时,代码可能很快复杂起来。
将列表转换为字典
用户输入和while循环
函数input()让程序暂停运行,等待用户输入一些文本。获取用户输入后,Python将其存储在一个变量中,Python将用户输入解读为字符串。
例如,下面的程序让用户输入一些文本,再将这些文本呈现给用户:
message = input("Tell me something, and I will repeat it back to you: ")
print(message)
- 函数input()接受一个参数,即要向用户显示的提示或说明。
- 程序等待用户输入,并在用户按回车键后继续运行。
编写清晰的程序
有时候,提示可能超过一行,例如,你可能需要指出获取特定输入的原因。这种情况下,可将提示存储再一个变量中,再将该变量传递给函数input()。
prompt = "If you tell us who you are, we can personalize the messages you see."
prompt += "\nwhat is your first name? "
name = input(prompt)
使用int()来获取数值输入
函数int()让Python将输入视为数值。
height = input("How tall are you, in inches? ")
height = int(height)
在Python 2.7 中获取输入
Python 2.7应使用函数raw_input()来提示用户输入,这个函数与Python 3 中的nput()一样,将输入解读为字符串。
Python 2.7 也包含函数input(),但它将用户输入解读为Python代码,并尝试运行它们。因此最好的结果是出现错误,指出Python不明白输入的代码;最糟糕的结果是,将运行原本无意运行的代码。
while循环简介
使用标志
在要求很多条件都满足才继续运行的程序中,可定义一个变量,用于判断真个程序是否处于活动状态,这个变量被称为标志。这样,在while语句中,只需检查一个条件——while的当前值是否为True。
active = True
while active:
message = input()
if message == 'quit':
active = false
else:
print(message)
使用 break 退出循环
while True:
city = input()
if city == 'quit':
break;
else:
print("xxxxx")
在循环中使用 continue
避免无限循环
如果程序陷入无限循环,可按Ctrl + C,也可关闭显示程序输出的终端窗口。
有些编辑器(如 Sublime Text)内嵌了输出窗口,这可能导致难以结束无限循环,因此不得不关闭编辑器来结束无限循环。
使用 While 循环来处理列表和字典
for循环是一种遍历列表的有效方式,但在for循环中不应修改列表,否则将导致Python难以跟踪其中的元素。要在遍历列表的同时对其进行修改,可使用while循环。将while循环同列表和字典结合起来使用,可收集、存储并组织大量输入,供以后查看和显示。
在列表之间移动元素
假设一个列表,其中包含新注册但还未验证的网站用户;验证这些用户后,如何将他们移到另一个已验证用户列表中呢?一种办法是使用一个while循环,在验证用户的同时将其从未验证用户列表中提取出来,再将其加入到另一个已验证用户列表中。
unconfirmed_users = ['alice', 'brian', 'candace']
confirmed_users = []
while unconfirmed_users:
current_user = unconfirmed_users.pop()
confirmed_user.append(current_user)
删除包含特定值的所有列表元素
在第3章中,我们使用方法remove()删除列表中的特定值(只删除第一个指定的值)。如果要删除列表中所有包含特定值的元素,该怎么办?
pets = ['dog', 'cat', 'dog', 'goldfish', 'cat', 'rabbit', 'cat']
while 'cat' in pets:
pets.remove('cat')
函数
现有函数
round(number, ndigits=None)
number:需要进行四舍五入的数字ndigits: 指定的位数,按此位数进行四舍五入
定义函数
下面是一个打印问候语的简单函数:
def greet_user():
"""显示简单的问候语"""
print("Hello!")
greet_user()
- 使用关键字def告诉Python要定义一个函数,定义以冒号结尾。
- 第二行的文本
"""显示简单的问候语"""是被称为文档字符串(docstring)的注释。文档字符串用三引号括起,Python用它们来生成有关程序中函数的文档
向函数传递信息
def greet_user(username):
"""显示简单的问候语"""
print("Hello, " + username.title() + "!")
greet_user('jesse')
传递实参
向函数传递实参的方式很多,可使用位置实参,这要求实参的顺序与形参的顺序相同;也可使用关键字实参,其中每个实参都由形参名和值组成;还可使用列表和字典。
关键字实参(顺序无关紧要)
def describe_pet(animal_type, pet_name):
"""显示宠物的信息"""
print("\nI have a " + animal_type + ".")
print("My " + animal_type + "'s name is " + pet_name.title() + ".")
describe_pet(animal_type='hamster', pet_name = 'harry')
默认值
编写函数时,可为每个形参指定默认值,那么在函数调用中就可以省略相应的实参。
def describe_pet(pet_name, animal_type='dog'):
"""显示宠物的信息"""
print("\nI have a " + animal_type + ".")
print("My " + animal_type + "'s name is " + pet_name.title() + ".")
describe_pet(pet_name='willie')
返回值
返回简单值
def get_formatted_name(first_name, last_name):
"""返回整洁的姓名"""
full_name = first_name + ' ' + last_name
return full_name.title()
musician = get_formatted_name('jimi', 'hendrix')
让实参变成可选的
def get_formatted_name(first_name, last_name, middle_name=''):
"""返回整洁的姓名"""
if middle_name:
full_name = first_name + ' ' + middle_name + ' ' + last_name
else:
full_name = first_name + ' ' + last_name
return full_name.title()
返回字典
def build_person(first_name, last_name, age=''):
"""返回一个字典,其中包含有关一个人的信息"""
person = {'first': first_name, 'last': last_name}
if age:
person['age'] = age
return person
musician = build_person('jimi', 'hendrix')
传递列表
假设有一个用户列表,我们要问候其中的每位用户。下面的示例将一个名字列表传递给一个名为greet_users()的函数,这个函数问候列表中的每个人:
def greet_users(names):
"""向列表中的每位用户都发出简单的问候"""
for name in names:
msg = "Hello, " + name.title() + "!"
print(msg)
usernames = ['hannah', 'ty', 'margot']
greet_users(usernames)
禁止函数修改列表
为了防止函数修改列表,可向函数传递列表的副本而不是原件。
要将列表的副本传递给函数,可以像下面这样做:
function_name(list_name[:])
虽然像函数传递列表的副本可保留原始列表的内容,但除非有充分的理由需要传递副本,否则还是应该将原始列表传递给函数。因为让函数使用现成列表可避免花时间和内存创建副本,从而提高效率,在处理大型列表时尤其如此。
传递任意数量的实参
有时候,你预先不知道函数需要接受多少个实参,好在Python允许函数从调用语句中收集任意数量的实参。
def make_pizza(*toppings):
"""打印顾客点的所有配料"""
print(toppings)
make_pizza('pepperoni')
make_pizza('mushrooms', 'green peppers', 'extra cheese')
- 形参名
*toppings中的星号*让Python创建一个名为toppings的空元组(用圆括号()标识,不可修改),并将收到的所有值都封装到这个元组中。
结合使用位置实参和任意数量实参
如果要让函数接受不同类型的实参,必须在函数定义中将接纳任意数量实参的形参放在最后。Python先匹配位置实参和关键字实参,再将余下的实参都收集到最后一个形参中。
例如,如果前面的函数还需要一个表示披萨尺寸的实参,必须将该形参放在形参*toppings前面:
def make_pizza(size, *toppings):
"""概述要制作的披萨"""
print("\nMaking a " + str(size) +
"-inch pizza with the following toppings:")
for topping in toppings:
print("- " + topping)
make_pizza(16, 'pepperoni')
make_pizza(12, 'mushrooms', 'green peppers', 'extra cheese')
使用任意数量的关键字实参
有时候,需要接受任意数量的实参,但预先不知道传递给函数的会是什么样的信息。可将函数编写成能够接受任意数量的 键-值 对——调用语句提供了多少就接受多少。
一个示例是创建用户简介:你知道将受到有关用户的信息,但不确定是什么样的信息。
def build_profile(first, last, **user_info):
"""创建一个字典,其中包含我们知道的有关用户的一切"""
profile = {}
profile['first_name'] = first
profile['last_name'] = last
for key, vaule in user_info.items():
profile[key] = value
return profile
user_profile = build_profile('albert', 'einstein',
location='princeton',
field='physics')
- 形参名
**user_info中的两个星号**让Python创建一个名为user_info的空字典(用花括号{}标识),并将收到的所有 名称-值 对都封装到这个字典中。
将函数存储在模块中
使用函数的优点之一是,使用它们可将代码块与主程序分离。通过给函数指定描述性名称,可让主程序容易理解得多。还可以更进一步,将函数存储在被称为模块的独立文件中,再将模块导入到主程序中。import语句允许在当前运行的程序文件中使用模块中的代码。
导入整个模块
要让函数是可导入的,得先创建模块。模块是扩展名为.py的文件,包含要导入到程序中的代码。
下面来创建一个包含函数make_pizza()的模块。为此,我们将文件pizza.py中除函数make_pizza()之外的其他代码都删除:
def make_pizza(size, *toppings):
"""概述要制作的披萨"""
print("\nMaking a " + str(size) +
"-inch pizza with the following toppings:")
for topping in toppings:
print("- " + topping)
接下来,我们在pizza.py所在的目录中创建另一个名为making_pizzas.py的文件,这个文件导入到刚创建的模块,再调用make_pizza()两次:
import pizza
pizza.make_pizza(16, 'pepperoni')
pizza.make_pizza(12, 'mushrooms', 'green peppers', 'extra cheese')
Python读取这个文件时,代码行import pizza让Python打开pizza.py,并将其中的所有函数都复制到这个程序中。
要调用被导入的模块中的函数,可指定导入的模块的名称pizza和函数名make_pizza(),并用句点分隔它们。如果你使用这种import语句导入了名为module_name.py的整个模块,就可使用下面的语法来使用其中任何一个函数:
module_name.function_name()
导入特定的函数
from module_name import function_0, function_1, function_2
- 通过逗号分隔函数名,可根据需要从模块中导入任意数量的函数
- 使用这种语法,调用函数时就无需使用句点
使用 as 给函数指定别名
要给函数指定别名,需要在导入时这样做。
from module_name import function_name as fn
- 上面的语句将函数
function_name()重命名为fn()
使用 as 给模块指定别名
import module_name as mn
导入模块中的所有函数
使用星号*运算符可让Python导入模块中的所有函数。
from pizza import *
make_pizza(16 'pepperoni')
import语句中的星号让Python将模块pizza中的每个函数都复制到这个文件中。由于导入了每个函数,可通过名称来调用每个函数,而无需使用句点表示法。然而,使用并非自己编写的大型模块时,最好不要采用这种导入方法:Python可能遇到多个名称相同的函数或变量,进而覆盖函数,而不是分别导入所有的函数。
最佳的做法是,要么只导入需要使用的函数,要么导入整个模块并使用句点表示法,这能让代码更清晰,更容易阅读和理解。
函数编写指南
给函数指定描述性名称,且只使用小写字母和下划线。
每个函数都应包含简要地阐述其功能的注释,该注释应紧跟在函数定义后面,并采用文档字符串格式。
给形参指定认值时,等号两边不要有空格
def function_name(parameter_0, parameter_1='default value')
对于函数调用中的关键字实参,等号两边不要有空格
function_name(value_0, parameter_1='value')
如果形参很多,导致函数定义的长度超过了79字符,可在函数定义中输入左括号后按回车键,并在下一行按两次Tab键,从而将形参列表和只缩进一层的函数体区分开来
def function_name(
parameter_0, parameter_1, parameter_2,
parameter_3, parameter_4, parameter_5):
function body...
如果程序或模块包含多个函数,可使用两个空行将相邻的函数分开,这样更容易知道前一个函数在什么地方结束,下一个函数从什么地方开始。
高阶函数
range() 还可指定步长
map()
def func(x):
return x*x
list(map(func, [1, 2, 3, 4, 5]))
a = [1, 2, 3, 4, 5]
list(map(str, map(func, a)))
匿名函数
使用lambda
lambda x:x*x
输入为x,输出为x*x
list(map(lambda x:x*x, [1, 2, 3, 4, 5]))
list(map(lambda x:'char is:'+str(x), [1, 2, 3, 4, 5]))
第三方包
import collections
a = [1, 2, 3, 1, 2, 31, 2, 1]
print(collections.Counter(a))
- csv
- datetime
- math
- pandas
- numpy
类
创建和使用类
创建 Dog 类
class Dog():
"""一次模拟小狗的简单尝试"""
def __init__(self, name, age):
"""初始化属性name和age"""
self.name = name
self.age = age
def sit(self):
"""模拟小狗被命令蹲下"""
print(self.name.title() + " is now sitting.")
def roll_over(self):
"""模拟小狗被命令时打滚"""
print(self.name.title() + " rolled over!")
- 根据约定,Python中首字母大写的名称指的是类。这个类定义中的括号是空的,因为我们要从空白创建这个类。
方法__init__()
类中的函数称为方法。就目前而言,函数和方法唯一重要的差别是调用方法的方式。
上例中的方法__init__()是一个特殊的方法,每当根据Dog类创建新实例时,Python都会自动运行它。
在这个方法名称中,开头和末尾各有两个下划线,这是一种约定,旨在避免Python默认方法与普通方法发生名称冲突。
这个方法的定义中,形参self必不可少,还必须位于其他形参的前面。
为何必须在方法定义中包含形参self呢?因为Python调用这个__init__()方法将自动传入实参self。每个与类相关联的方法调用都自动传递实参self,它是一个指向实例本身的引用,让实例能够访问类中的属性和方法。
我们创建Dog实例时,Python将调用Dog类的方法__init__()。我们将通过实参向Dog()传递name和age,self会自动传递。
以self为前缀的变量都可供类中的所有方法使用,我们还可以通过类的任何实例来访问这些变量。
self.name = name获取存储在形参name中的值,并将其存储到变量name中,然后该变量被关联到当前创建的实例。
像这样可以通过实例访问的变量称为属性。
sit()和roll_over()方法不需要额外的信息,因此它们只有一个形参self。
在 Python 2.7 中创建类
在 Python 2.7 中创建类时,需要做细微的修改——在括号内包含单词object:
class ClassName(object):
根据类创建实例
my_dog = Dog('willie', 6)
遇到上述代码时,Python使用实参willie和6调用Dog类中的方法__init__()。方法__init__()并未显式地包含return语句,但Python自动返回一个表示这条小狗的实例。在这里,命名约定很有用:我们通常可以认为首字母大写的名称指的是类,小写的名称指的是根据类创建的实例。
访问属性
my_dog.name,在Dog类中引用这个属性使用的是self.name
调用方法
my_dog.sit()
my_dog.roll_over()
使用类和实例
Car 类
class Car():
"""一次模拟汽车的简单尝试"""
def __init__(self, make, model, year):
"""初始化描述汽车的属性"""
self.make = make
self.model = model
self.year = year
def get_descriptive_name(self):
"""返回整洁的描述性信息"""
long_name = str(self.year) + ' ' + self.make + ' ' + self.model
return long_name.title()
my_new_car = Car('audi', 'a4', 2016)
print(my_new_car.get_descriptive_name())
运行结果:
2016 Audi A4
给属性指定默认值
class Car():
def __init__(self, make, model, year):
"""初始化描述汽车的属性"""
self.make = make
self.model = model
self.year = year
self.odometer_reading = 0
def get_descriptive_name(self):
--snip--
def read_odometer(self):
"""打印一条指出汽车里程的消息"""
print("This car has " + str(self.odometer_reading) + " miles on it.")
my_new_car = Car('audi', 'a4', 2016)
print(my_new_car.get_descriptive_name())
my_new_car.read_odometer()
修改属性的值
直接修改属性的值
my_new_car.odometer_reading = 23
通过方法修改属性的值
class Car():
--snip--
def update_odometer(self, mileage):
"""将里程表读数设置为指定的值"""
self.odometer_reading = mileage
my_new_car = Car('audi', 'a4', 2016)
print(my_new_car.get_descriptive_name())
my_new_car.update_odometer(23)
my_new_car.read_odometer()
可对方法update_odometer()进行扩展,禁止任何人将里程表读数往回调:
class Car():
--snip--
def update_odometer(self, mileage):
"""
将里程表读数设置为指定的值
禁止将里程表读数往回调
"""
if mileage >= self.odometer_reading:
self.odometer_reading = mileage
else:
print("You can't roll back an odometer!")
通过方法对属性的值进行递增
class Car():
--snip--
def update_odometer(self, mileage):
--snip--
def increment_odometer(self, miles):
"""将里程表读数增加指定的量"""
self.odometer_reading+= miles
继承
一个类继承另一个类时,它将自动获得另一个类的所有属性和方法。原有的类称为父类,新类称为子类。子类同时还可以定义自己的属性和方法。
子类的方法__init__()
创建子类的实例时,Python首先需要给父类的所有属性赋值,为此,子类的方法__init__()需要父类施以援手。
下面来创建一个简单的ElectricCar类版本,它具备Car类的所有功能:
class ElectricCar(Car):
"""电动汽车的独特之处"""
def __init__(self, make, model, year):
"""初始化父类的属性"""
super().__init__(make, model, year)
my_tesla = ElectricCar('tesla', 'model s', 2016)
print(my_tesla.get_descriptive_name())
- 创建子类时,父类必须包含在当前文件中,且位于子类前面。
- 定义子类时,必须在括号内指定父类的名称。
super()是一个特殊函数,帮助Python将父类和子类关联起来。父类也称为超类(superclass),名称super因此而得名。
Python 2.7 中的继承
在Python 2.7 中,继承语法稍有不同。
class Car(object):
def __init__(self, make, model, year):
--snip--
class ElectricCar(Car):
def __init__(self, make, model, year):
super(ElectricCar, self).__init__(make, model, year)
- 函数
super()需要两个实参:子类名和对象self。
给子类定义属性和方法
class ElectricCar(Car):
"""电动汽车的独特之处"""
def __init__(self, make, model, year):
"""
电动汽车的独特之处
初始化父类的属性,再初始化电动汽车特有的属性
"""
super().__init__(make, model, year)
self.battery_size = 70
def describe_battery(self):
"""打印一条描述电瓶容量的消息"""
print("This car has a " + str(self.battery_size) + "-kwh battery.")
my_tesla = ElectricCar('tesla', 'model s', 2016)
my_tesla.describe_battery()
重写父类的方法
对于父类的方法,只要它不符合子类模拟的实物的行为,都可对其进行重写。为此,可在子类中定义一个与要重写的父类方法同名的方法。
假设Car类有一个名为fill_gas_tank()的方法,它对全电动汽车来说毫无意义。下面演示一种重写方式:
class ElectricCar(Car):
--snip--
def fill_gas_tank(self):
"""电动汽车没有油箱"""
print("This car doesn't need a gas tank!")
使用继承时,可让子类保留从父类继承而来的精华,并剔除不需要的糟粕。
将实例用作属性
使用代码模拟实物时,可能会发现给类添加的细节越来越多:属性和方法清单以及文件都越来越长。这种情况下,可能需要将类的一部分作为一个独立的类提取出来,将大型类拆分称多个协同工作的小类。
例如,不断给ElectricCar类添加细节时,我们可能会发现其中包含很多专门针对汽车电瓶的属性和方法。可以将这些属性和方法提取出来,放到另一个名为Battery的类中,并将一个Battery实例用作ElectricCar类的一个属性:
class Car():
--snip--
class Battery():
"""一次模拟电动汽车电瓶的简单尝试"""
def __init__(self, battery_size=70):
"""初始化电瓶的属性"""
self.battery_size = battery_size
def describe_battery(self):
"""打印一条描述电瓶容量的消息"""
print("This car has a " + str(self.battery_size) + "-kwh battery.")
class ElectricCar(Car):
"""电动汽车的独特之处"""
def __init__(self, make, model, year):
"""
初始化父类的属性,再初始化电动汽车特有的属性
"""
super().__init__(make, model, year)
self.battery = Battery()
my_tesla = ElectricCar('tesla', 'model s', 2016)
my_tesla.battery.describe_battery()
这看似做了很多额外的工作,但现在我们想多详细地描述电瓶都可以,且不会导致ElectricCar类混乱不堪。
导入类
Python允许将类存储在模块中,然后在主程序中导入所需的模块(模块是扩展名为.py的文件,包含要导入到程序中的代码)。
导入单个类
下面是模块car.py,其中只包含Car类的代码:
"""一个可用于表示汽车的类"""
class Car():
"""一次模仿汽车的简单尝试"""
def __init__(self, make, model, year):
"""初始化描述汽车的属性"""
self.make = make
self.model = model
self.year = year
self.odometer_reading = 0
def get_descriptive_name(self):
"""返回整洁的描述性名称"""
long_name = str(self.year) + ' ' + self.make + ' ' + self.model
return long_name.title()
def read_odometer(self):
"""打印一条消息,指出汽车的里程"""
print("This car has " + str(self.odometer_reading) + " miles on it.")
def update_odometer(self. mileage):
"""
将里程表读数设置为指定的值
拒绝将历程表往回拨
"""
if mileage >= self.odometer_reading:
self.odometer_reading = mileage
else:
print("You can't roll back an odometer!")
def increment_odometer(self, miles):
"""将里程表读数增加指定的量"""
self.odometer_reading += miles
下面创建另一个文件——my_car.py,在其中导入Car类并创建其实例:
from car import Car
my_new_car = Car('audi', 'a4', 2016)
print(my_new_car.get_descriptive_name())
my_new_car.odometer_reading = 23
my_new_car.reading_odometer()
导入类是一种有效的编程方式,让大部分逻辑存储在独立的文件中,使主程序文件变得整洁而易于阅读。
在一个模块中存储多个类
虽然同一个模块中的类之间应存在某种相关性,但可根据需要在一个模块中存储任意数量的类。
类Battery和ElectricCar都可以帮助模拟汽车,因此可以将其加入模块car.py中。
从一个模块中导入多个类
from car import Car, ElectricCar
导入整个模块
可以导入整个模块,再使用句点表示法访问需要的类。这中导入方法很简单,代码也易于阅读。由于创建类实例的代码都包含模块名,因此不会与当前文件使用的任何名称发生冲突。
import car
my_beetle = car.Car('volkswagen', 'beetle', 2016)
my_tesla = car.ElectricCar('tesla', 'roadster', 2016)
导入模块中的所有类
要导入模块中的每个类,可使用下面的语法:
from module_name import *
但是不推荐这种导入方式(同导入模块中的所有元素),原因有二:
- 这种导入方式没有明确地指出你使用了模块中的哪些类。
- 还可能引发名称方面的困惑。如果不小心导入了一个与程序文件中其他东西同名的类,将引发难以诊断的错误。
需要从一个模块中导入很多类时,最好导入整个模块,并用module_name.class_name语法来访问类。
在一个模块中导入另一个模块
有时候,需要将类分散到多个模块中,以免模块太大,或在同一个模块中存储不相关的类。将类存储在多个模块中时,你可能会发现一个模块中的类依赖于另一个模块中的类。这种情况下,可在前一个模块中导入必要的类。
例如,下面将Car类存储在一个模块中,并将ElectricCar和Battery类存储再另一个模块中。我们将第二个模块命名为electric_car.py:
"""一组可用于表示电动汽车的类"""
from car import Car
class Battery():
--snip--
class ElectricCar(Car):
--snip--
现在可以分别从每个模块中导入类,以根据需要创建任何类型的汽车了:
from car import Car
from electric_car import ElectricCar
my_beetle = Car('volkswagen', 'beetle', 2016)
print(my_beetle.get_descriptive_name())
my_tesla = ElectricCar('tesla', 'roadster', 2016)
print(my_tesla.get_descriptive_name())
Python 标准库
Python标准库是一组模块,安装好的Python都包含它。可使用标准库中的任何函数和类,为此只需在程序开头包含一条简单的import语句。
下面来看模块collection中的一个类——OrderedDict。要创建字典并记录其中的键-值对的添加顺序,即可使用模块collections中的OrderedDict类。再来看一看第6章的favorite_languages.py示例:
from collections import OrderedDict
favorite_languages = OrderedDict()
favorite_languages['jen'] = 'python'
favorite_languages['sarah'] = 'c'
favorite_languages['edward'] = 'ruby'
favorite_languages['phil'] = 'python'
for name, language in favorite_languages.items():
print(name.title() + "'s favorite language is " +
language.title() + ".")
这是一个很不错的类,它兼具列表和字典的主要优点(在将信息关联起来的同时保留原来的顺序)。
模块random
模块random包含以各种方式生成随机数的函数,其中的randint()返回一个位于指定范围内的整数。
例如,下面的代码返回一个1~6内的整数:
from random import randint
x = randint(1, 6)
类编码风格
- 类名:应采用驼峰命名法。
- 实例名和模块名:应采用小写格式,并在单词之间加上下划线。
- 在类中,可使用一个空行来分隔方法;在模块中,可使用两个空行来分隔类。
- 需要同时导入标准库中的模块和自己编写的模块时,先编写导入标准库模块的import语句,再添加一个空行,然后编写导入自己编写的模块的import语句。这种做法让人更容易明白程序使用的各个模块来自何方。
文件和异常
从文件中读取数据
文本文件可存储的数据量多的难以置信,每当需要分析或修改存储在文件中的信息时,读取文件都很有用,对数据分析应用程序来说尤其如此。例如可以编写一个这样的程序:读取一个文本文件的内容,重新设置这些数据的格式并将其写入文件,让浏览器能够显示这些内容。
要使用文本文件中的信息,首先需要将信息读取到内存中。为此,可以一次性读取文件的全部内容,也可以每次一行逐步读取。
读取整个文件
首先创建一个文件,它包含精确到小数点后30位的圆周率值,且在小数点后每10位处都换行:
3.1415926535
8979323846
2643383279
将上述文件保存为pi_digits.txt,保存到本章程序所在的目录中。
下面的程序打开并读取这个文件,再将其内容显示到屏幕上:
with open('pi_digits.txt') as file_object:
contents = file_object.read()
print(contents)
再这个程序中,第一行代码做了大量的工作:
文件路径
Python默认在当前执行的文件所在的目录中查找指定的文件,但有时可能要打开不在程序文件所属目录中的文件。要让Python打开不与程序文件位于同一个目录中的文件,需要提供文件路径。
逐行读取
读取文件时,常常需要检查其中的每一行:你可能要在文件中查找特定的信息,或者要以某种方式修改文件中的文本。例如,你可能要遍历一个包含天气数据的文件,并使用天气描述中包含字样sunny的行;在新闻报道中,你可能会查找包含标签<headline>的行,并按特定的格式设置它。
要以每次一行的方式检查文件,可对文件对象使用for循环:
filename = 'pi_digits.txt'
with open(filename) as file_object:
for line in file_object:
print(line)
我们打印每一行时,发现空白行更多了:
3.1415926535
8979323846
2643383279
为什么会出现这些空白行呢?因为在这个文件中,每行的末尾都有一个看不见的换行符,而print语句也会加上一个换行符。要消除这些多余的空白行,可在print语句中使用rstrip():print(line.rstrip())
创建一个包含文件各行内容的列表
使用关键字with时,open()返回的文件对象只在with代码块内可用。如果要在with代码块外访问文件的内容,可在with代码块内将文件的各行存储在一个列表中,并在with代码块外使用该列表:
filename = 'pi_digits.txt'
with open(filename) as file_object:
lines = file_object.readlines()
for line in lines:
print(line.rstrip())
- 方法
readlines()从文件中读取每一行,并将其存储在一个列表中。
使用文件的内容
首先创建一个字符串,它包含文件中存储的所有数字,且没有任何空格:
filename = 'pi_digits.txt'
with open(filename) as file_object:
lines = file_object.readlines()
pi_string = ''
for line in lines:
pi_string += line.rstrip()
print(pi_string)
print(len(pi_string))
打印结果:
3.1415926535 8979323846 2643383279
36
在变量pi_string存储的字符串中,包含原来位于左边的空格,为删除这些空格,**可使用strip()**而不是rstrip()
注意:
读取文本文件时,Python将其中的文本都解读为字符串。如果读取的是数字,并要将其作为数值使用,就必须使用函数int()或float()转换为数字。
包含小数点后一百万位的大型文件
只要系统内存足够多,想处理多少数据都可以。
圆周率值中包含你的生日吗
为确认某个人的生日是否包含在圆周率值得前1 000 000位中,可将生日表示为一个由数字组成得字符串,再检查这个字符串是否包含在pi_string中:
filename = 'pi_digits.txt'
with open(filename) as file_object:
lines = file_object.readlines()
pi_string = ''
for line in lines:
pi_string += line.strip()
birthday = input("Enter your birthday, in thje form mmddyy: ")
if birthday in pi_string:
print("Your birthday appears in the first million digits of pi!")
else:
print("Your birthday does not appear in the first million digits of pi.")
写入文件
保存数据最简单的方式之一是将其写入到文件中。
写入空文件
要将文本写入文件,在调用open()时需要提供另一个实参,告诉Python要写入打开的文件。
filename = 'programming.txt'
with open(filename, 'w') as file_object:
file_object.write("I love programming.")
实参'w'告诉Python,我们要以写入模式打开这个文件。
打开文件时,可指定模式
- 读取模式(‘r’)
- 写入模式(‘w’)
- 附加模式(‘a’)
- 读写模式(‘r+’)
如果省略了模式实参,默认以只读模式打开文件。
如果要写入的文件不存在,函数open()将自动创建它。然而,以写入(‘w’)模式打开文件时千万要小心,因为如果指定的文件已经存在,Python将在返回文件对象前清空该文件。
文件对象的方法write()将一个字符串写入文件。
Python只能将字符串写入文本文件,要将数值数据存储到文本文件中,必须先使用函数str()将其转换为字符串格式。
写入多行
函数write()不会在写入的文本末尾添加换行符,要让每个字符串都单独占一行,需要在write()语句中包含换行符。
附加到文件
如果要给文件添加内容,而不是覆盖原有内容,可以**附加模式(‘a’)**打开文件。如果指定的文件不存在,Python会创建一个空文件。
filename = 'programming.txt'
with open(filename, 'a') as file_object:
file_object.write("I also love finding meaning in large datasets.\n")
file_object.write("I love creating apps that can run in a browser.\n")
异常
Python使用被称为异常的特殊对象来管理程序执行期间发生的错误。每当发生让Python不知所措的错误时,它都会创建一个异常对象。如果编写了处理该异常的代码,程序将继续运行;如果未对异常进行处理,程序将停止,并显示一个traceback,其中包含有关异常的报告。
异常是使用try-except代码块处理的。try-except代码块让Python执行指定的操作,同时告诉Python发生异常时怎么办。使用了try-except代码块时,即便出现异常,程序也将继续运行:显示编写的友好的错误消息,而不是令用户迷惑的traceback。
使用 try-except 代码块
当你认为可能发生了错误时,可编写一个try-except代码块来处理可能引发的异常。
处理ZeroDivisionError异常的try-except代码块类似于下面这样:
try:
print(5/0)
except ZeroDivisionError:
print("You can't divide by zero!")
使用异常避免崩溃
发生错误时,如果程序还有工作没有完成,妥善地处理错误就尤其重要。这种情况经常会出现在要求用户提供输入的程序中;如果程序能够妥善地处理无效输入就能再提示用户提供有效输入,而不至于崩溃。
else 代码块
将可能引发错误地代码放在try-except代码块中,可提高这个程序抵御错误的能力。依赖于try代码块成功执行的代码都应放到else代码块中:
try:
answer = int(first_number) / int(second_number)
except ZeroDivisionError:
print("You can't divide by 0!")
else:
print(answer)
处理 FileNotFoundError 异常
filename = 'alice.txt'
try:
with open(filename) as f_obj:
contents = f_obj.read()
except FileNotFoundError:
msg = "Sorry, the file " + filename + " does not exist."
print(msg)
如果文件不存在,这个程序什么都不做,因此错误处理代码的意义不大。
分析文本
下面来提取童话Alice in Wonderland的文本,并尝试计算它包含多少个单词。
我们将使用方法split(),它根据一个字符串创建一个单词列表。方法split()以空格为分隔符将字符串分拆成多个部分,并将这些部分都存储在一个列表中。
filename = 'alice.txt'
try:
with open(filename) as f_obj:
contents = f_obj.read()
except FileNotFoundError:
msg = "Sorry, the file " + filename + " does not exist."
print(msg)
else:
words = contents.split()
num_words = len(words)
print("The file " + filename + " has about " + str(num_words) + " words.")
使用多个文件
下面多分析几本书。我们先将这个程序的大部分代码移到一个名为count_words()的函数中,这样对多本书进行分析时将更容易:
def count_words(filename):
"""计算一个文件大致包含多少个单词"""
try:
with open(filename) as f_obj:
contents = f_obj.read()
except FileNotFoundError:
msg = "Sorry, the file " + filename + " does not exist."
print(msg)
else:
words = contents.split()
num_words = len(words)
print("The file " + filename + " has about " + str(num_words) + " words.")
filename = 'alice.txt'
count_words(filename)
失败时一声不吭
要让程序在失败时一声不吭,可通过pass语句,在except代码块中明确表明什么都不做:
def count_words(filename):
"""计算一个文件大致包含多少个单词"""
try:
--snip--
except FileNotFoundError:
pass
else:
--snip--
pass语句还充当了占位符。它提醒你在程序的某个地方什么都没有做,并且以后也许要在这里做些什么。在这个程序中,我们可能决定将找不到的文件的名称写入到文件missing_files.txt中。
使用 模块json 存储数据
很多程序要求用户输入某种信息,如让用户存储游戏首选项或提供可视化的数据。不管专注的是什么,程序都把用户提供的信息存储在列表和字典等数据结构中。用户关闭程序时,几乎总是要保存他们提供的信息,一种简单的方式是使用模块json来存储数据。
- 模块json能将简单的Python数据结构转储到文件中,并在程序再次运行时加载该文件中的数据。
- 还可以使用json在Python程序之间分享数据
- JSON数据格式不是Python专用,因此能够将以JSON格式储的数据与使用其他编程语言的人分享
- JSON是一种轻便格式,很有用,也易于学习
- **JSON(JavaScript Object Notation)**格式最初是为JavaScript开发的,但随后成了一种常见格式,被众多语言采用
我们来编写程序,使用json.dump()来存储一组数字,使用json.load()将这些数字读取到内存中。
使用 json.dump()
- 函数
json.dump()接受两个实参:
- 要存储的数据
- 可用于存储数据的文件对象
import json
numbers = [2, 3, 5, 7, 11, 13]
filename = 'numbers.json'
with open(filename, 'w') as f_obj:
json.dump(numbers, f_obj)
- 先导入模块json,再创建一个数字列表。
- 通常使用文件扩展名
.json来指出文件存储的数据为JSON格式。
- 使用函数
json.dump()将数字列表存储到文件numbers.json中
使用 json.load()
import json
filename = 'numbers.json'
with open(filename) as f_obj:
numbers = json.load(f_obj)
print(numbers)
保存和读取用户生成的数据
来看这样一个例子:用户首次运行程序时被提示输入自己的名字,这样再次运行程序时就记住他了。
先存储用户的名字:
import json
username = input("What is your name? ")
filename = 'username.json'
with open(filename, 'w') as f_obj:
json.dump(username, f_obj)
print("We'll remember you when you come back, " + username + "!")
再编写一个程序,向其名字被存储的用户发出问候:
import json
filename = 'username.json'
with open(filename) as f_obj:
username = json.load(f_obj)
print("Welcome back, " + username + "!")
我们需要将这两个程序合并到一个程序中。这个程序运行时,我们将尝试从文件username.json中获取用户名。因此首先编写一个尝试恢复用户名的try代码块。如果这个文件不存在,我们就在except代码块中提示用户输入用户名,并将其存储在username.json中,以便程序再次运行时能够获取它:
import json
filename = 'username.json'
try:
with open(filename) as f_obj"
username = json.load(f_obj)
except FileNotFoundError:
username = input("What is your name? ")
with open(filename, 'w') as f_obj:
json.dump(username, f_obj)
print("We'll remember you when you come back, " + username + "!")
else:
print("Welcome back, " + username + "!")
重构
你经常会遇到这样的情况:代码能够正确地运行,但可做进一步的改进——将代码划分为一系列完成具体工作的函数。这样的过程被称为重构。重构让代码更清晰、更易于理解、更容易扩展。
要重构上述程序,可将大部分逻辑放到一个或多个函数中。
import json
def greet_user():
"""问候用户,并指出其名字"""
filename = 'username.json'
try:
with open(filename) as f_obj:
username = json.load(f_obj)
except FileNotFoundError:
username = input("What is your name? ")
with open(filename, 'w') as f_obj:
json.dump(username, f_obj)
print("We'll remember you when you come back" + username + "!")
else:
print("Welcome back, " + username + "!")
greet_user()
下面来重构greet_user(),让它不执行这么多任务:
import json
def get_stored_username():
"""如果存储了用户名,就获取它"""
filename = 'username.json'
try:
with open(filename) as f_obj:
username = json.load(f_obj)
except FileNotFoundError:
return None
else:
return username
def get_new_username():
"""提示用户输入用户名"""
username = input("What is your name? ")
filename = 'username.json'
with open(filename. 'w') as f_obj:
json.dump(username, f_obj)
def greet_user():
"""问候用户,并指出其名字"""
username = get_stored_username()
if username:
print("Welcom back, " + username + "!")
else:
username = get_new_username()
print("We'll remember you when you come back" + username + "!")
greet_user()
在这个版本中,每个函数都执行单一而清晰的任务。
测试代码
测试函数
下面是一个简单的函数,它接受名和姓并返回整洁的姓名:
def get_formatted_name(first, last):
"""生成整洁的姓名"""
full_name = first + ' ' + last
return full_name.title()
为核实函数像期望的那样工作,来编写一个使用这个函数的程序:
from name_function import get_formatted_name
print("Enter 'q' at any time to quit.")
while True:
first = input("\nPlease give me a forst name: ")
if first == 'q':
break
last = input("Please give me a last time: ")
if last == 'q':
break
formatted_name = get_formatted_name(first, last)
print("\tNeatly formatted name: " + formatted_name + '.')
现在假设我们要修改get_formatted_name(),使其还能处理中间名。这样做时,我们要确保不破坏这个函数处理只有名和姓的姓名的方式。为此,我们可以在每次修改get_formatted_name()后都进行测试:运行程序names.py,并输入像Janis Joplin这样的姓名,但这太繁琐了。所幸Python提供了一种自动测试函数输出的高效方式。
单元测试和测试用例
Python标准库中的模块unittest提供了代码测试工具。
- 单元测试:用于核实函数的某个方面没有问题
- 测试用例:是一组单元测试,这些单元测试一起核实函数在各种情形下的行为都符合要求。
良好的测试用例考虑到了函数可能收到的各种输入,包含针对所有这些情形的测试。全覆盖式测试用例包含一整套单元测试,涵盖了各种可能的函数使用方式。对于大型项目,要实现全覆盖很难。通常,最初只要针对代码的重要行为编写测试即可,等项目被广泛使用时再考虑全覆盖。
可通过的测试
创建测试用例的语法需要一段时间才能习惯,但测试用例创建后,再添加针对函数的单元测试就很简单了。要为函数编写测试用例,可先导入模块unittest以及要测试的函数,再创建一个继承unittest.TestCase的类,并编写一系列方法对函数行为的不同方面进行测试。
下面是一个只包含一个方法的测试用例,它检查函数get_formatted_name()在给定名和姓时能否正确地工作:
import unittest
from name_function import get_formatted_name
class NamesTestCase(unittest.TestCase):
"""测试name_function.py"""
def test_first_last_name(self):
"""能够正确地处理像Janis Joplin 这样的姓名吗? """
formatted_name = get_formatted_name('janis', 'joplin')
self.assertEqual(formatted_name, 'Janis Joplin')
unittest.main()
代码行unittest.main()让Python运行这个文件中的测试:
.
---------------------------------------------------------
Ran 1 test in 0.000s
OK
- 第一行的句点
.表明有一个测试通过了
- 最后的OK表明该测试用例中的所有单元测试都通过了
测试类的命名最好让它看起来与要测试的函数相关,并包含字样Test。这个类必须继承unittest.TestCase类,这样Python才知道如何运行你编写的测试。
我们运行上述程序时,所有以test_打头的方法都会自动运行。
unittest最有用的功能之一:一个断言方法。
断言方法用来核实得到的结果是否与期望的结果一致(应该满足的条件是否确实满足)。上述代码通过调用unittest的方法assertEqual(),并向它传递formatted_name和'Janis Joplin'。
不能通过的测试
测试未通过时结果是什么样的呢?我们来修改get_formatted_name(),使其能够处理中间名,但这样做时,故意让这个函数无法正确地处理像Janis Joplin这样只有名和姓的姓名。
下面是函数get_formatted_name()的新版本,它要求通过一个实参指定中间名:
def get_formatted_name(first, middle, last):
"""生成整洁的姓名"""
full_name = first + ' ' + middle + ' ' + last
return full_name.title()
这次运行测试代码,将会得到如下输出:
E
=======================================================
ERROR: test_first_last_name (__main__.NamesTestCase)
------------------------------------------------------
...
...
...
------------------------------------------------------
Ran 1 test in 0.000s
FAILED (errors=1)
- 第一行字母E指出测试用例中有一个单元测试导致了错误。
- 最后一行指出整个测试用例都未通过,因为运行该测试用例时发生了一个错误。
添加新测试
我们再编写一个测试,用于测试包含中间名的姓名。为此,在NamesTestCase类中再添加一个方法:
import unittest
from name_function import get_formatted_name
class NamesTestCase(unittest.TestCase):
"""测试name_function.py"""
def test_first_last_name(self):
"""能够正确地处理像Janis Joplin 这样的姓名吗? """
formatted_name = get_formatted_name('janis', 'joplin')
self.assertEqual(formatted_name, 'Janis Joplin')
def test_first_last_middle_name(self):
"""能够正确地处理像Wolfgang Amadeus Mozart这样的姓名吗? """
formatted_name = get_formatted_name(
'wolfgang', 'mozart', 'amadeus')
self.assertEqual(formatted_name, 'Wolfgang Amadeus Mozart')
unittest.main()
- 测试方法名必须以
test_打头,这样它才会在我们运行test_name_function.py时自动运行。
- 可以在TestCase类中使用很长的方法名,这些方法名必须是描述性的,这样才能让你明白测试未通过时的输出。
两个测试都通过的输出:
..
-------------------------------------------------
Ran 2 tests in 0.000s
OK
测试类
各种断言方法
Python在unittest.TestCase类中提供了很多断言方法。
6个常用的断言方法:
| 方法 |
用途 |
assertEqual(a, b) |
核实a == b |
assertNotEqual(a, b) |
核实a != b |
assertTrue(x) |
核实x为True |
| assertFalse(x) |
核实x为False |
assertIn(item, list) |
核实item在list中 |
assertNotIn(item, list) |
核实item不在list中 |
一个要测试的类
类的测试与函数的测试相似——所做的大部分工作都是测试类中方法的行为,但存在一些不同之处,下面来编写一个类进行测试。
来看一个帮助管理匿名调查的类:
class AnonymousSurvey():
"""收集匿名调查问卷的答案"""
def __init__(self, question):
"""存储一个问题,并为存储答案做准备"""
self.question = question
self.responses = []
def show_questinon(self):
"""显示调查问卷"""
print(self.question)
def store_response(self, new_response):
"""存储单份调查答卷"""
self.responses.append(new_response)
def show_results(self):
"""显示收集到的所有答卷"""
print("Survey results:")
for response in self.responses:
print('- ' + response)
为证明AnonymousSurvey类能够正确地工作,我们来编写一个使用它地程序:
from survey import AnonymousSurvey
question = "What language did you first learn to speak?"
my_survey = AnonymousSurvey(question)
my_survey。show_question()
print("Enter 'q' at any time to quit.\n")
while True:
response = input("Language: ")
if response == 'q':
break
my_survey.store_response(response)
print("\nThank you to everyone who participated in the survey!")
my_survey.show_results()
AnonymousSurvey类可用于进行简单的匿名调查。假设我们将它放在了模块survey中,并想进行改进:让每位用户都可输入多个答案;编写一个方法,它只列出不同的答案,并指出每个答案出现了多少次;再编写一个类,用于管理非匿名调查。
进行上述修改存在风险,可能会影响AnonymousSurvey类的当前行为。要确认在开发这个模块时没有破坏既有行为,可以编写针对这个类的测试。
测试 AnonymousSurvey 类
下面来编写一个测试,对AnonymouSurvey类的行为进行验证:如果用户面对调查问题时只提供了一个答案,这个答案也能被妥善地存储;用户提供三个答案时,也将被妥善地存储:
import unittest
from survey import AnonymousSurvey
class TestAnonymousSurvey(unittest.TestCase):
"""针对AnonymousSurvey类的测试"""
def test_store_single_response(self):
"""测试单个答案会被妥善地存储"""
question = "What language did you first learn to speak?"
my_survey = AnonymousSurvey(question)
my_survey.store_response('English')
self.assertIn('English', my_survey.responses)
def test_store_three_responses(self):
"""测试三个答案会被妥善地存储"""
question = "What language did you first learn to speak?"
my_survey = AnonymousSurvey(question)
responses = ['English', 'Spanish', 'Mandarin']
for response in responses:
my_survey.store_response(response)
for response in responses:
self.assertIn(response, my_survey.responses)
unittest.main()
上述做法的效果很好,但这些测试有些重复的地方。下面使用unittest的另一项功能来提高它们的效率。
方法 setUp()
unittest.TestCase类中包含了方法setUp()。让我们只需创建这些对象一次,并在每个测试方法中使用它们。如果在TestCase类章包含了方法setUp(),Python将先运行它,再运行各个以test_打头的方法。这样,在每个测试方法中都可使用在方法setUp()中创建的对象了。
下面使用setUp()来创建一个调查对象和一组答案,供方法test_store_single_response()和test_store_three_responses()使用:
import unittest
from survey import AnonymousSurvey
class TestAnonymousSurvey(unittest.TestCase):
"""针对AnonymousSurvey类的测试"""
def setUp(self):
"""
创建一个调查对象和一组答案,供使用的测试方法使用
"""
question = "What language did you first learn to speak?"
self.my_survey = AnonymousSurvey(question)
self.responses = ['English', 'Spanish', 'Mandarin']
def test_store_single_response(self):
"""测试单个答案会被妥善地存储"""
self.my_survey.store_response(self.responses[0])
self.assertIn(self.responses[0], self.my_survey.responses)
def test_store_three_responses(self):
"""测试三个答案会被妥善地存储"""
for response in self.responses:
self.my_survey.store_response(response)
for response in self.responses:
self.assertIn(response, self.my_survey.responses)
unittest.main()
方法setUp()做了两件事:
- 创建一个调查对象
- 创建一个答案列表
存储这两样东西的变量名包含前缀self(即存储在属性中),因此可在这个类的任何地方使用。
测试自己编写的类时,方法SetUp()让测试方法编写起来更容易:可在setUp()方法中创建一系列实例并设置它们的属性,再在测试方法中直接使用这些实例。
注意:
运行测试用例时,每完成一个单元测试,Python都打印一个字符:测试通过时打印一个句点;测试引发错误时打印一个E;测试导致断言失败时打印一个F。
Python项目
数据可视化